Hello Steemians, I’m @vandeberg, Senior Blockchain Developer at Steemit and today I want to do a more technical deep dive in to the rewards system of Steem and shed some light on the nuances of changing a reward curve. We recently proposed changing the reward curve to a "convergent linear rewards curve" as part of the effort to improve the economics of Steem. What does that mean?

To read more about how the Steemit team believes the economics of Steem can be improved, check out this post on @steemitblog.

ELI5

When Steem was first created, rewards were distributed based on a “superlinear” rewards curve. That meant that accounts with a lot of Steem Power had more innate influence on a per-Steem-basis than smaller accounts. That curve was very effective at encouraging people to consolidate their Steem into one account, which made it easy for other users to find and respond to bad actors. But a side effect of this curve was that the “rich got richer” at a rate which made the ecosystem feel extremely unfair.

Switching to a linear rewards curve meant that every account had the same degree of influence (on a per-Steem-basis) on the rewards pool regardless of the total amount of Steem they had in their accounts. At the time most felt that this dramatically improved the fairness of the ecosystem, and since that change was put into place, we have seen a reduction in the income inequality in Steem. One problem with this change was that it reduced the incentive to consolidate one’s stake in a single account, which made it easier for bad actors to divide up their stake and hide their activities.

Reward Mechanics

To gain a deeper understanding of how these different curves function, let’s look at a few hypothetical scenarios and see how they play out based on how much stake the users have, and the type of curve that is in place.

When a comment is 7 days old, it is rewarded based on the number of reward shares (or rshares) it has, modified by some function called a rewards curve. Steem currently has a linear rewards curve, which means the rshares are modified by the curve f(x) = mx + b. Specifically Steem uses the curve f(x) = x where the rshares are not changed at all. This is compared to a moving total of rshares recently paid out. Let's work through a simple example.

Let's say that Alice authored a post that received 10 rshares. The pool of recent rshares contains 1000 rshares, and the reward fund holds 100.000 STEEM. The reward curve is applied to Alice's 10 rshares, giving us 10 rshares and those are added to the total recent rshares, giving us 1010 rshares. Then Alice is rewarded with 10/1010 of the reward fund, or 9.900 STEEM. The actual values on the blockchain are much different than this, but the math is the same. In addition, the recent rshares are decayed slightly each block. Over time it reaches a pseudo-equilibrium which normalizes rewards over time.

With the same constraints, what if Bob had a comment rewarded at the same time, but he only had 5 rshares. Both of their rshares would be added to the total recent rshares for a value of 1015. Alice would be rewarded with 10/1015 of the reward fund for 9.985 STEEM and Bob would be rewarded with 5/1015 of the reward fund for 4.926 STEEM. As you can see, Alice's comment had twice as many rshares voting for it and she received twice as much STEEM as Bob. We might also call this a proportional rewards curve because the rewards are proportional to the number of rshares voting for a piece of content.

The Different Curves

When Steem was first launched we had an n^3 reward curve, which was changed to n^2 before the first payouts began on July 4th, 2016. Let's run the example again but with a rewards curve of n^2. To make the values somewhat close, we also need to increase the size of the recent rshares to 5000. We have to add an extra step in the calculation that was implicit before, the application of the rewards curve. Alice's comment has 10 rshares, but when we apply that to f(n) = n^2 we get an actual value of 100. Doing the same to Bob's comment gives us a value of 25, for a new total recent rshares of 5125.

Now, Alice is rewarded with 100/5125 of the reward pool, or 19.512 STEEM, whereas Bob is rewarded 25/5125 of the reward pool, or 4.878 STEEM, four times less than Alice! We call this a superlinear reward curve. Certainly this is not fair. Steemit and the witnesses agree, which is why we changed the rewards curve to linear on June 20, 2017 in Hardfork 19.

Superlinearity

However, there is a really nice property of a super linear reward curve. It encourages consolidating stake in order to maximize rewards. In the Steem Whitepaper we refer to this as "anti-sybil". The scenario that it seeks to combat is a single entity spreading their stake over many small accounts in order to hide their actions in noise. A single entity doing this can hide their intentions and siphon off small rewards over time and be difficult to detect. Superlinear rewards incentivizes consolidating stake or at least having the smaller accounts act together, which makes the behavior much more difficult to hide if the entity wants to act in an optimal manner.

Best of Both Worlds?

Is there a way for us to capture the fairness of linear rewards and keep the anti-sybil benefits of superlinearity? We believe so with what we have termed the convergent linear rewards curve. This curve is of the form n^2 / (n + 1).

Let's look at the example above again, but add in Charlie who has a comment with 20 rshares. We will go back to a recent rshare value of 1000. We will also be using the specific reward curve of n^2 / (n/5 + 1) for this example.

Alice has 10 rshares which are augmented by the rewards curve to be 33 rshares.
Bob has 5 rshares which are augmented by the rewards curve to be 12 rshares.
Charlie has 20 rshares which are augmented by the rewards curve to be 80 rshares.

The payouts then for Alice would be 29.333 STEEM. Bob would be 10.666 STEEM. Charlie would be 71.111 STEEM.

Looking at Alice and Bob, Alice only has twice as many rshares as Bob, but was rewarded with 2.75 times as much STEEM, an increase of 37.5% STEEM per rshare.

However, while Charle also has twice as many rshares as Alice, he was only rewarded with 2.42 times as much STEEM, an increase of 21% STEEM per rshare.

That is the beauty of this curve! As more rshares are awarded to comments, the marginal gain (percent STEEM per rshare) decreases. However, the actual STEEM reward per rshare still increases. If it did not, we would see Charlie rewarded with less than 2 times as much STEEM as Alice, resulting in a negative percent STEEM per rshare.

We have decided to call this a convergent linear rewards curve, because as the number of rshares increases, this curve converges on linearity and behaves more and more like a linear rewards curve. The specific curve it behaves like can be derived by calculating the limit at infinity. In the case of this curve, it behaves like the curve f(n) = 10n. We can tune how quickly the curve converges to the equivalent linear rewards curve by changing the coefficient of the denominator term.

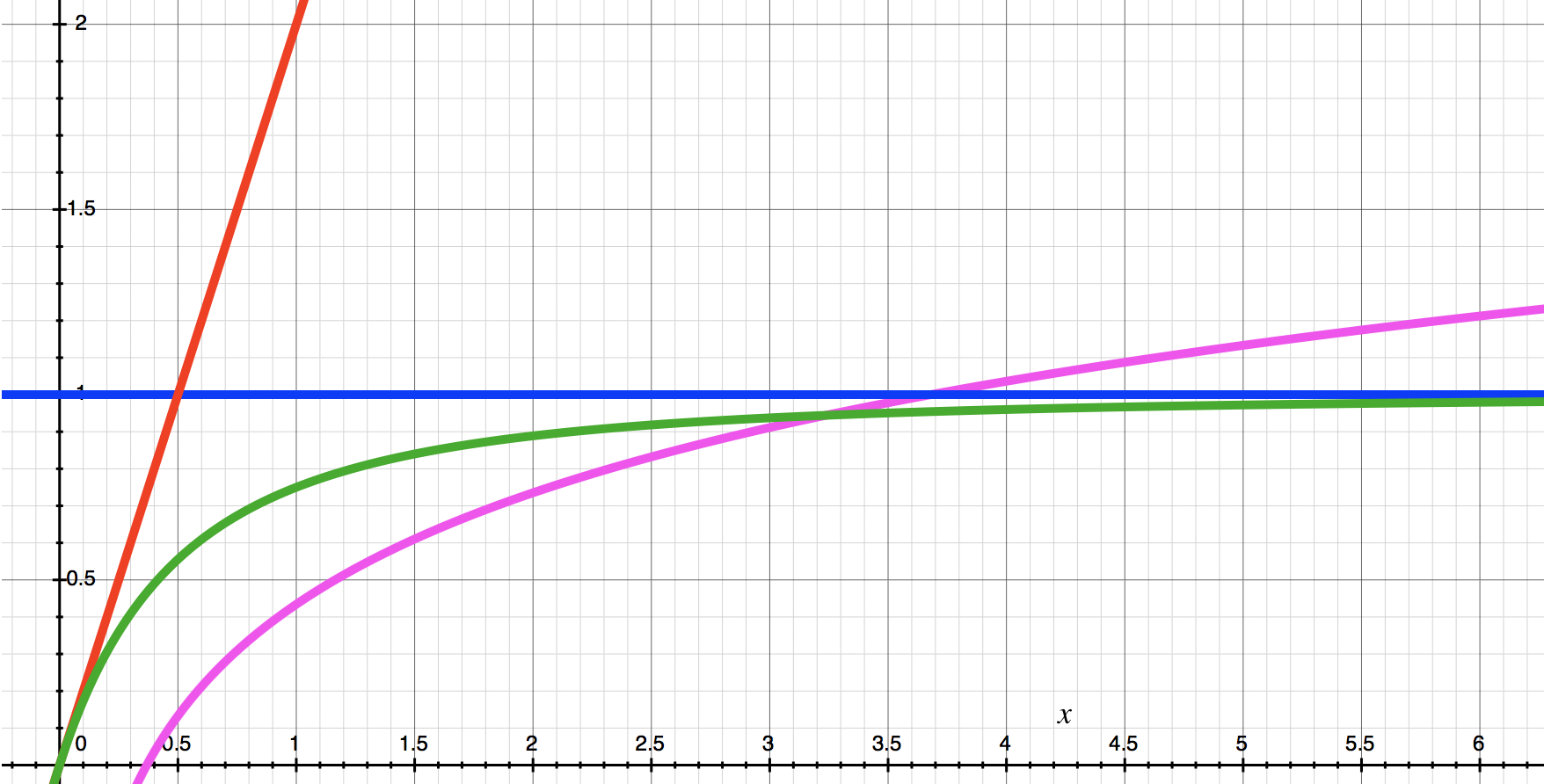
We can graph the derivatives of the reward curves to visualize their "fairness" over time. The red line is n^2, the blue line is n, green is n^2 / (n + 1), and pink is n log( n ). The pink line was added as another point of comparison because it is a common function that grows faster than n but slower than n^2 and is a reasonable candidate for a superlinear curve. This graph confirms what our intuition is regarding these curves from the previous examples. n^2 continues to get more and more unfair as rshares increase and n is fair regardless of rshares. The green curve for n^2/(n+1) is cool because you can see it start unfair with n^2 and end fair with n. n log(n) continues to grow forever. While it is not as unfair as n^2 it does continue to grow in unbounded unfairness, while n^2 / (n+1) does not.

The goal of this post was to deep dive into one of the critical pieces of the Economic Improvement Proposal. Let me know if you have any questions in the comments section below, or what part of the proposal I should “deep dive” into next.

Vandeberg