SLC21 Week4 - Recursion

Hello steemians,

Here is my homework for SLC21 Week 4, with the corresponding tasks assigned by @sergeyk!

_{Edited by Canva}

Describe recursion as you understand it. Have you encountered recursion before?

Recursion is when a function calls itself until it reaches a stopping condition, it then stops calling itself. The result of each child function is returned to the parent functions, until it returns to the original function, this explanation may not be entirely clear right away, but it will become so!

The very concept of recursion is relatively simple in truth. It is the implementation that bugs many developers, to unblock all that, we will start right away by making a first high level diagram of the concept.

I want you to have a mental image of what we are talking about before even starting to look at code.

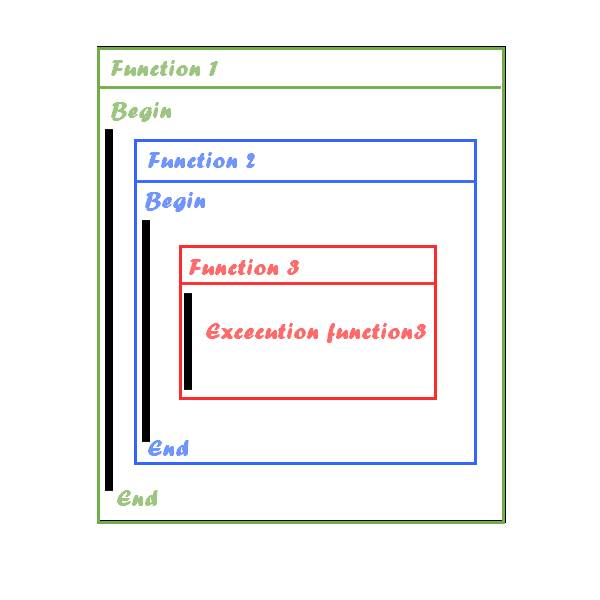
I want you to immediately integrate a key concept in recursion: when a function calls itself, the child function is part of the execution of the parent function. In other words, the execution of each function is nested more and more deeply with each call.

The first time I was taught recursion, I was immediately given the famous Fibonacci sequence as an example. I wanted to do the same today and then I remembered how complicated I had found it as an introduction. Because of that, using recursion impressed me for a long time. I found it almost surreal as a concept.

How is the word "fractal" related to recursion?

A fractal is composed of figures identical to itself but on a reduced scale. This is a concept closely related to recursion. An example of such a figure is the Sierpinski triangle.

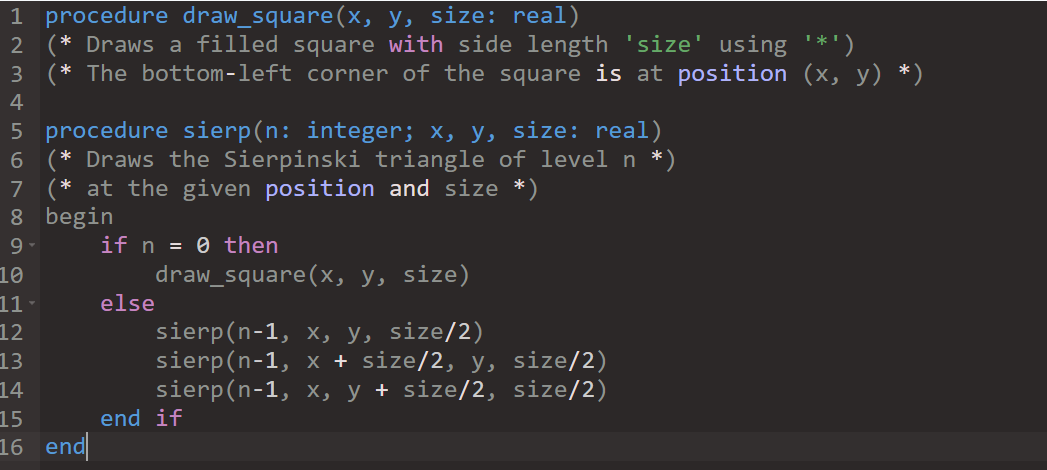
The Sierpinski triangle at level 0 is a simple filled square, of a given size. To go to level 1, we decompose the square into four half-sized squares and “leave aside” the square at the top right (figure 1(a)). To go to level 2, we repeat the operation for these three squares (figure 1(b)) and so on.

Such fractal figures are very easy to draw with recursive algorithms. The above procedure draws the Sierpinski triangle at a given level n.

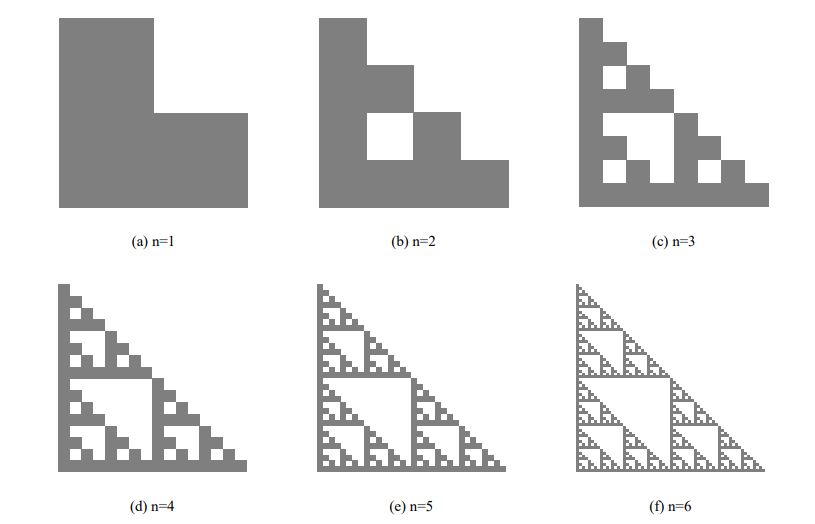
Explore the limit of what is the largest value of the factorial that can be calculated with a certain type of data.

To determine the largest factorial value that can be calculated for different data types, we can look at the maximum number of a data type that can be stored and find the largest factorial within that limit.

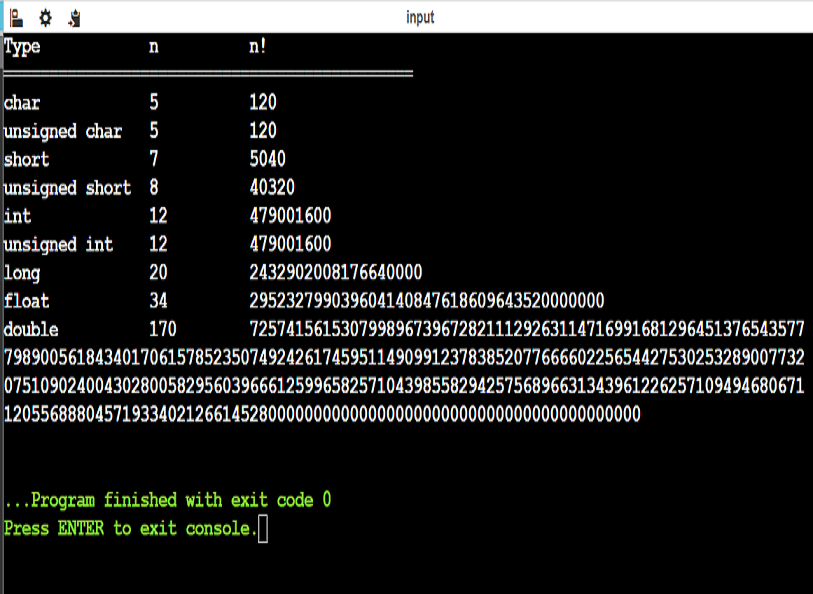
Below is a Python script that determines the maximum factorial n! for common data types (char, int, float, short, long, double) based on their size and range.

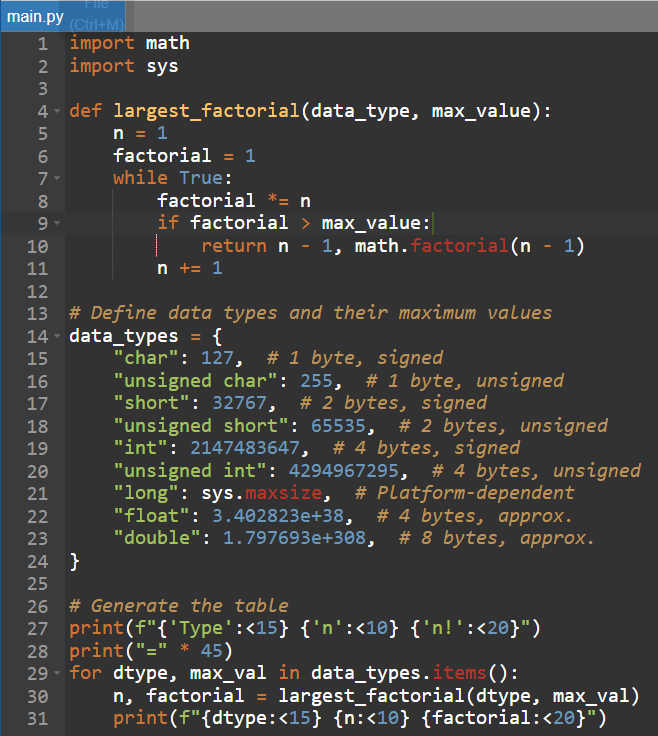The limits of computable factorials for different data types depend on the maximum storage capacity of each type, for example a signed char type with a range of -128 to 127 can calculate factorials only up to 5! because 6! exceeds 127.

For larger types like int or long the limits increase considerably a signed int can handle up to 12! before 13! exceeds its maximum capacity of 2147483647.

Floating point types like float and double allow much larger factorials to be computed due to their ability to represent much larger numbers although at the cost of losing precision, for example a float can represent approximately 34! before hitting limits while a double with much higher capacity can reach up to 170! before accuracy is compromised.

These limits are crucial in contexts where the calculations involve factorials because choosing an inappropriate type could lead to overshoots or erroneous results.

Investigate how many calls the function will make before it terminates. This task is described in more detail in the lecture.

Let's look at the simplest example I can use to explain this concept. We're going to count backwards starting from 2. Yes, I know, we're being too crazy, watch your eyes, here we go.

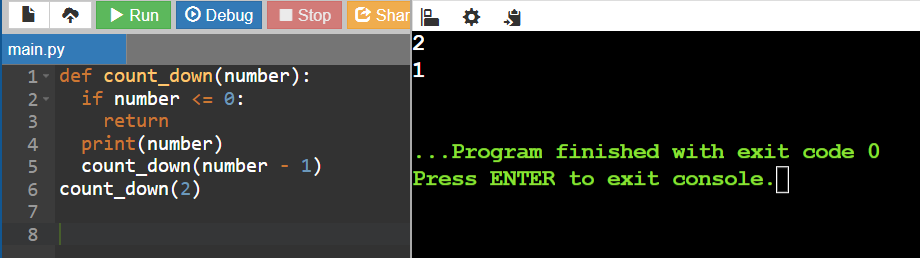
To do this, we will detail each step of this algorithm. There are three main steps for each recursive algorithm.

• The stop condition
• The resolution of the problem
• The recursive call

We will base ourselves on the piece of code in Javascript for the explanation:

Stop condition (line 2)

When you write a recursive function, the first thing you want to do is to check if the recursion must stop. In other words, if the function must no longer call itself. This condition is mandatory! Without it, it will be a mess very quickly.

condition

Here, it is very simple, our stop case is when the number we are counting reaches 0 or below. If the current number is 0, our count is finished and we stop the recursion by immediately exiting the current function with a return (line 3).

Solving the problem (line 4)

Here our problem is simple: we just want to display the current number. We do it nonchalantly on line 4 with a print.

The recursive call (line 5)
For the recursion to work, the heart of the concept is that the function calls itself during its execution. This is exactly what we do here on line 5.

It is also important to understand that this is where we subtract a unit from the number we are counting (in the function call parameter). If we don't do it, we will display the same number each time, and above all, we will do it infinitely!!

So that you understand what is happening in this function I will take the high-level diagram above. But this time, I will apply what we have just seen in the piece of code to count.

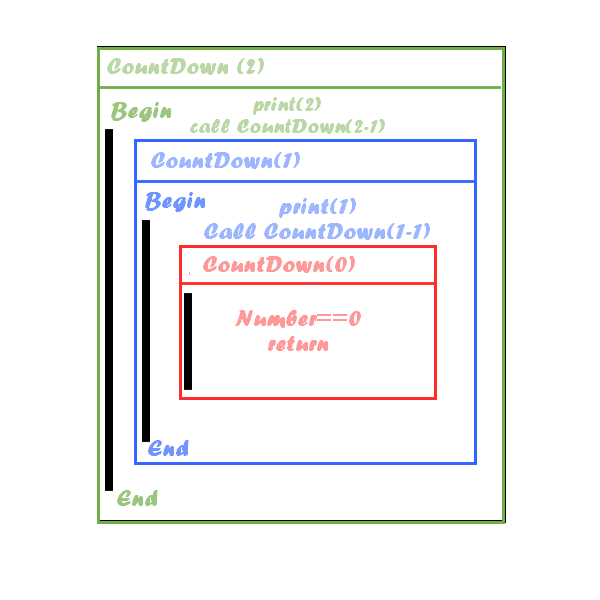
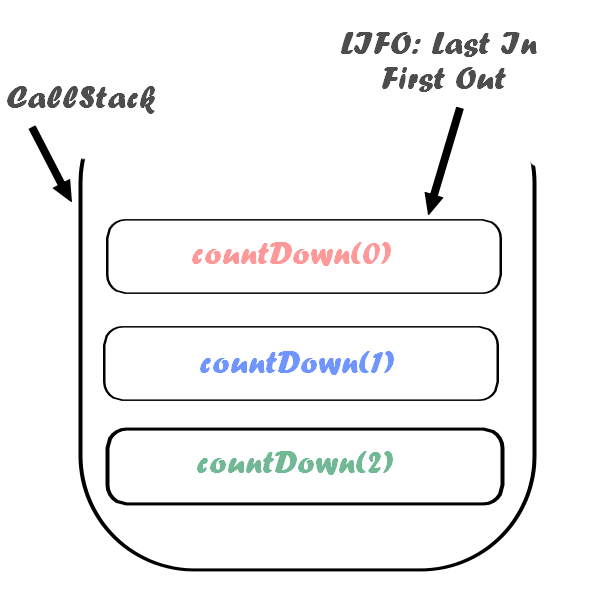
Recursion uses what is called the execution stack for its operation. The execution stack has the same operation as a traditional stack, except that it manages the active functions of the program. In other words, when a program calls a function, this function goes on top of the call stack.

And so, as the operation of a stack requires, the function at the top of the stack will be the first to be executed. That is to say that the last function called will be the one executed. Let's draw a picture using the previous example to make it clearer.

Print the numbers from 1 to n.

I implemented a print_numbers_recursive function to print numbers from 1 to n using a recursive approach, for this case the stopping condition is that n is less than 1, when this condition is met the function no longer does nothing and goes back to the previous call level.

The main idea behind this recursive function is to exploit the order of recursive calls to print numbers in ascending order, when calling print_numbers_recursive(n - 1), the function continues to remember itself with decreasing values of n, until n reaches 0, once this condition is reached, the recursion stops, and the recursive calls start to go back and forth each When returning, the number n of the current level is printed.

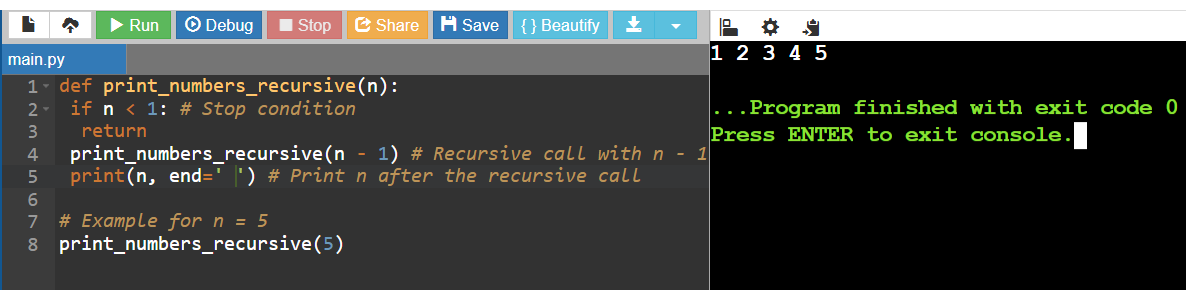
For n = 5 , here's what happens:

1. Successive calls: print_numbers_recursive(5) → print_numbers_recursive(4) → print_numbers_recursive(3) → print_numbers_recursive(2) → print_numbers_recursive(1) → print_numbers_recursive(0).
2. Stop condition: When n = 0 , the function returns without doing anything.
3. Returns and prints: When each call returns, the corresponding number is printed, producing the numbers in ascending order: 1, 2, 3, 4, 5.

This method exploits the nature of the recursion call stack to print the numbers in the desired order, making it elegant and suitable for this type of problem.

Print numbers from n to 1.

This code defines a function called print_numbers_recursive_desc that prints numbers from n to 1 using recursion, the function relies on the idea that it calls itself with a slightly reduced problem until a stopping condition is reached the stopping condition here is when n becomes less than 1 in which case the function stops executing and goes back to the previous level before making the recursive call, The function prints the current number n followed by a space which displays all numbers on a single line.

When called with n = 5, for example, the function first prints 5, then calls itself with n - 1, i.e. 4, and so on until 1, once n = 0, the stopping condition is met and the function stops, thus completing the display sequence, the order of the recursive calls ensures that the numbers are displayed in descending order without requiring a loop explicit.

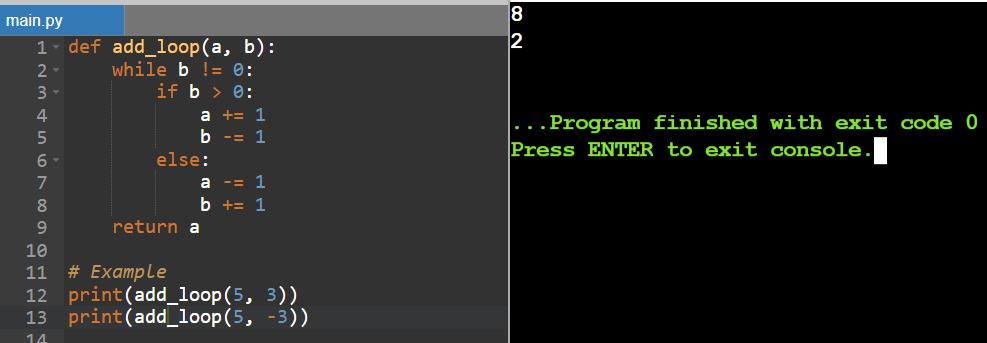
Write a function to calculate the sum of two numbers a+b. Do not use the a+b calculation directly. First perform this task using a loop (1 point), maybe it will tell you how to use recursion here and perform this task

Here I wrote a function to calculate the sum of two numbers a and b without directly using the + operator, I first used a loop to accomplish this task, incrementing or decrementing a based on the value of b, in the case if b is positive I keep adding 1 to a while reducing b by 1 until b reaches 0 and if b is negative I decrement a and increment b by 1 so similar until b is zero.

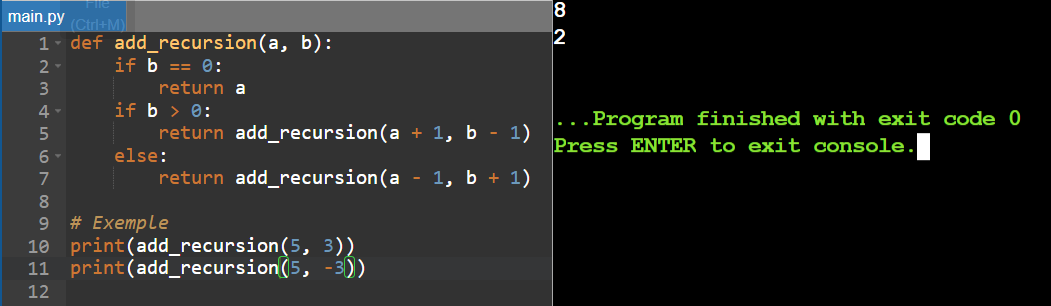
Then I used a recursive approach to accomplish the same task, if b is 0 I simply return a as that means the sum is complete, if b is positive I increment a and call the function back in diminishing b and if b is negative, I decrement a and I increment b.

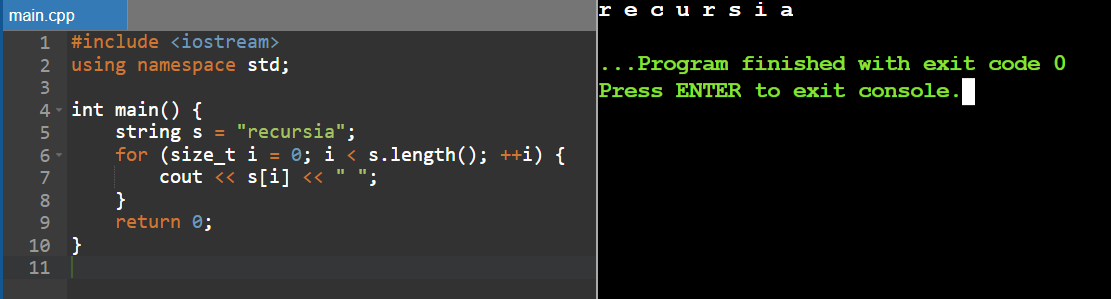
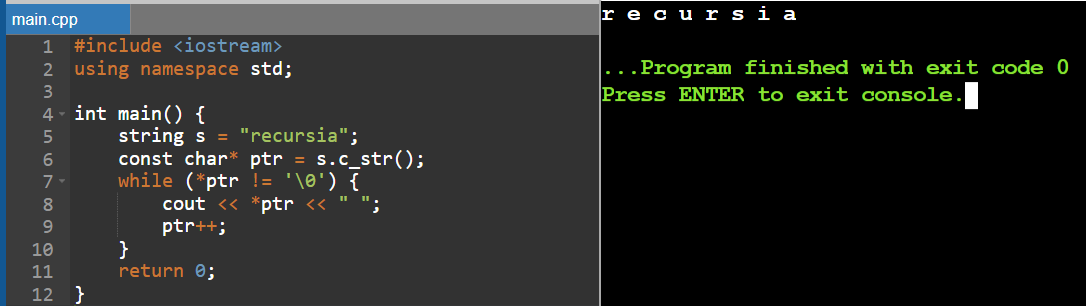
Print a string character by character (as an array). Remember that when declaring a string char s[]="recursia"; s is not the string itself - it is the address of its first character, the address of the array. And to print a character at the address stored in s you can do this printf("%c", s[0]); or printf("%c", *s); - if s is the address of a character array (string), then s[0] is its first character. And the entry *s means to dereference the pointer - that is, to get the value located at the address s For those who know C++ - it is easier here - just print through cout either s[0] or *s. I will add one more hint: if s is the address of the first character - then s+1 is the address of the second)))

Using a Loop

In C++, a string can be treated as an array of characters, allowing us to print each character sequentially by iterating through its indices. This method accesses characters from the start of the string and prints them one by one.

Example Code in C++:

Using Pointer Dereferencing

Another approach involves using pointer dereferencing to traverse and print the string. By treating the string as a sequence of characters in memory, a pointer can access and print each character by moving through the string one position at a time.

Example Code in C++:

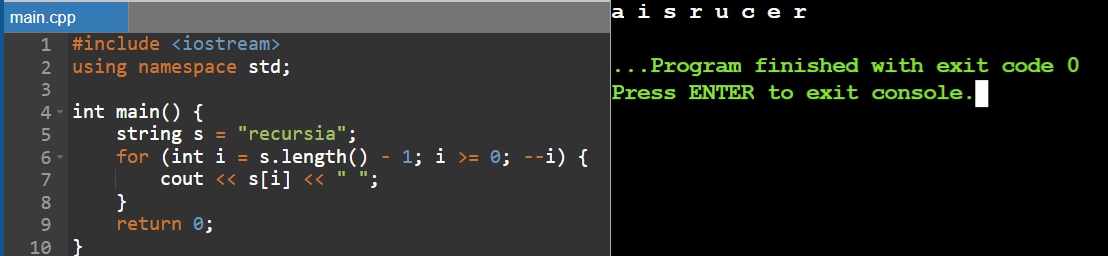
Similar to the previous task - but the line must be displayed backward, turned around.

Printing in Reverse Using a Loop

To print a string in reverse order, we can iterate backward, starting from the last character and moving toward the first. This requires determining the string's length and decrementing an index to access each character in reverse.

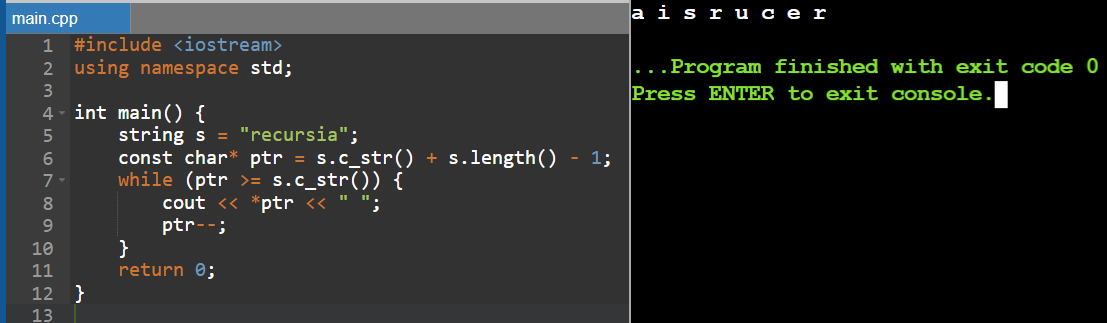
Printing in Reverse Using Pointer Dereferencing

We can also reverse a string by using pointers. This method moves a pointer to the end of the string and iterates backward by decrementing the pointer, accessing and printing each character at the pointer's location.

Example Code in C++:

---

Thank you very much for reading, it's time to invite my friends @analp, @crismenia, @eliany to participate in this contest.

Best Regards,
@kouba01