Simulating a Steem curation rewards distribution that is modeled after a 2nd price auction
10 comments
This post describes some simulated results from a curation distribution algorithm that was inspired by the concept of a second-price auction.
Introduction

pixabay license: source

pixabay license: source
Some time ago, I had a conversation with @personz about the desirability of self-voting. I hope I'm not mis-characterizing the argument*, but as I recall, the position that @personz took was that self-voting conveys no information to the blockchain, so it should be considered equivalent to noise or spam. This led to the conclusion that all authors should abstain from self-voting.
(* - Clarification: "argument" as in "logical argument". The conversation was not at all confrontational.)
On the other hand, my position was that voting can be abused, whether by self or others, and the self-vote is a perfectly valid form of expression, provided that it's sincerely given in reflection of the merit of the content. In my own view, self-voting is ok, but it doesn't absolve the voter of the obligation to put an honest appraisal on the value of one's own post.
Of course, this is a long-standing topic of conversation among Steemizens, and I'm not trying to reopen the debate in this post, but I'd like to revisit that conversation in another context.
While we were talking, I said that it reminded me of the karate tournaments that @cmp2020 used to attend. In those tournaments, 5 judges would submit their scores, the lowest and highest scores would be thrown out, and the contestant would receive the average of the scores from the remaining 3 judges. This methodology eliminated outliers whose votes were wildly out of step with the judging consensus. I said I wondered if something similar could mitigate the harm from abusive votes (by self and others) in the Steem curation consensus.
Either during that conversation, or thinking about the karate tournaments & Steem voting shortly afterwards, I was reminded of an article that I had read some time before which indicated that Google had done some extensive game theory research with the problem of fair ranking in its Ad Words product, and the best solution they found was the 2nd price auction.
And there things stood. I have mentioned in a number of comments since that time that I thought it might be a good idea to explore this concept, but basically left it to others to figure out what a voting algorithm based upon a second price auction would even look like. Of course, this guaranteed that the idea would be ignored.
So, last week, I finally thought that I would go ahead and write a rewards simulator to see how a voting algorithm could even be modeled after the concept of a second price auction. Here's what I found.

What is a second price auction?
Simply put, in the second price auction, the winner of the auction is the person that bids the most, but the price they pay is not the price that they bid. Instead, the price they pay is the 2nd highest bid that was submitted.
As I recollect, the reason that Google chose this algorithm for their Ad Words product, is because of a convenient mathematical property, stated here on gametheory.net:
The theoretical nicety of second price auctions, first pointed out by William Vickrey, is that bidding one's true value is a dominant strategy
So the question is, can we find a curation rewards calculation that acts in similar fashion to the karate tournament scoring by weeding out outliers and like a 2nd-price auction by incentivizing voters to vote correctly (according to their own perceptions)?

How does this apply to Steem voting?
After commenting repeatedly that I wonder if there is a solution to Steem's curation problem in an algorithm that's modeled after a second price auction, I decided that I should take the idea past "hand-waving." In this context, what does "modeled after" even mean?
So last week, I wrote a shell script to loosely simulate basic curation rewards on a Steem post. (It ignores the reverse auction for early voting and negative voting) Once I had it so that it seemed to be close to matching actual payouts, I made a modified version that would accept the current voting information and calculate rewards as-if generated through a second price auction inspired algorithm.
In this version, the voting is all the same, but the rshares from the highest voter get thrown back into the rewards pool. The payouts are then calculated based on the total after those rshares get subtracted. This means that the highest and earliest voters still win the distribution, but the reward payment amounts are made as if the highest voter hadn't voted. Each voter gets credit for the rshares from the next-highest voter, with the exception of the lowest voter (in rshares), who gets credit for their own rshares - unless they're the only voter, then they get 0. (yeah, that seems like a kludge, but I just wanted to "sketch" the idea out.)
Using that script, here are the top 10 potential curation rewards on one of today's trending posts:
R E W A R D S
current | simulated
---------- ----------
21.187692 | 3.132037
11.524 | 10.155
11.08 | 16.51
10.0770 | 9.67429
6.268 | 5.795
2.5009 | 2.0895
1.190127 | 0.836698
0.461401 | 0.194006
0.447819 | 0.295523
0.2631 | 0.1247
And here is the same information from a post with a high amount of self-voting:
R E W A R D S
current | simulated
---------- ----------
5.665636 | 0.274980
1. | 0.3
0.505638 | 0.046393
0.309271 | 0.091192
0.148121 | 0.160000
0.147017 | 0.051299
0.069935 | 0.030932
0.0494 | 0.0188
0.039489 | 0.015661
0.036847 | 0.014599
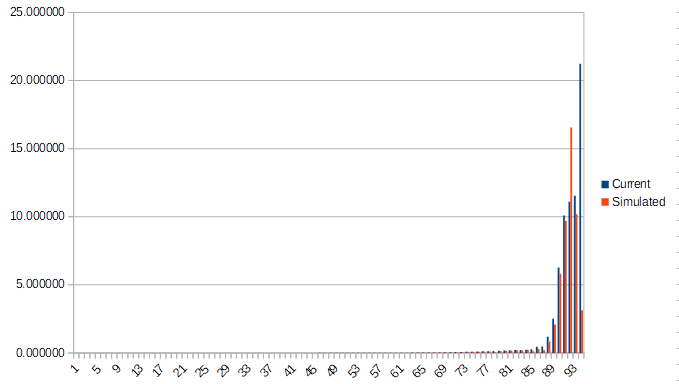
From the same trending post, here is a graph of current and simulated rewards, sorted by highest payout under the actual algorithm.
And here is a similar graph from the post with a high self-vote.
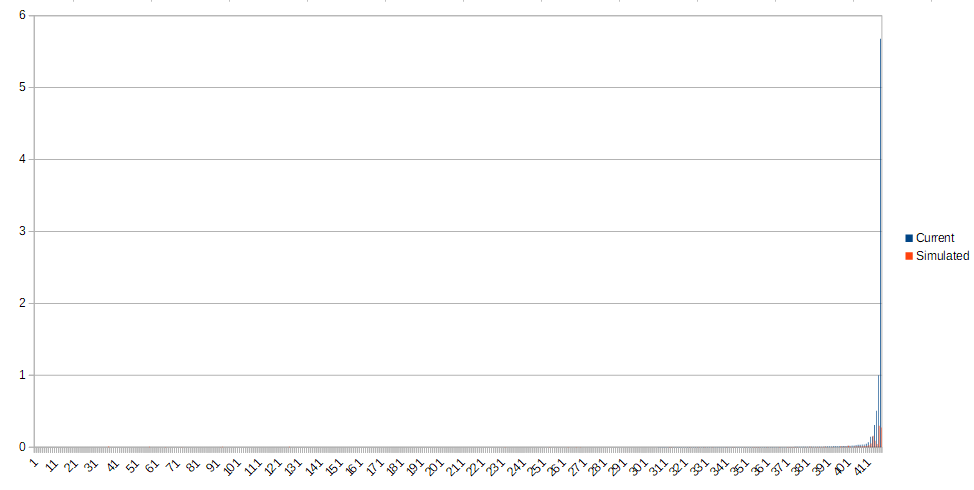
As you can see, in both posts, the outlier votes are drastically reduced, but voters who are inside the consensus range don't change as much. By punishing the outlier like that, it creates an incentive for a voter not to vote too far away from other voters - you know that even if you "win", your rewards are being calculated from someone else's vote, and it also creates a requirement that a post must get at least 2 votes to receive a payout.

Discussion
Of course, the simulator hasn't been validated and it can't predict how people's behavior would change in response to the methodological change. It also doesn't account for all the rshares getting put back into the reward pool. But, in order to "game" this algorithm, the abusive voter would need to divide their stake into 2 or more separate accounts, and they would have to be willing to sacrifice all of the rshares from one account. So while it may not be perfect, it seems that it may create a disincentive against abusive voting, whether by self or others.
It is also interesting that Steemit proposed the convergent linear solution in the days after I wrote this script. Since that proposal creates an incentive not to split one's stake, it might be interesting to see how these two proposals interact with each other.
I don't claim that this is a final answer to Steem's problem with inaccurate post ranking, but I do think that it may be worthy of further consideration.
Addendum: Here is the original conversation, in this post by @rycharde. Looks like I was mistaken to think that it first came up in our conversations about self-voting..
Thank you for your time and attention.
As a general rule, I up-vote comments that demonstrate "proof of reading".
Steve Palmer is an IT professional with three decades of professional experience in data communications and information systems. He holds a bachelor's degree in mathematics, a master's degree in computer science, and a master's degree in information systems and technology management. He has been awarded 3 US patents.
Steve is also a co-founder of the Steem's Best Classical Music Facebook page, and the @classical-music steemit curation account.
Follow in RSS: @remlaps, @remlaps-lite


Comments