"SLC-S22W1/Variables and Expressions"
11 comments
Task # 1 |
|---|
Explain any two variables and expression types other than those that are explained in this course. (Practical and algebraic examples are required!)
This is the symbolic representation of a value that can be varied or altered. Mostly, alphabets are used to showcase the variables.
Let's say we have a bucket containing different numbers of mangoes, we can say that bucket has "a" number of mangoes similarly "2a" means twice the number of mangoes and so on
➡️Example:
4a+ 3b
here, "a" and "b" are variables and represent any value, while 4 and 3 are coefficients.
Types of variables
Here, I choose two different types of variables other than those mentioned in the lecture.
🔷️Extraneous variables
These variables are not part of the study or research but can affect the outcomes or results. For example, if you open an egg shop, your sales are dependent on the buying power of customers, but if this egg shop is in front of gum, then the bodybuilders' demand can increase your profit. So, the demand for builders is an extraneous variable which affects the resultant profit.
🔹️Practical example:
My father owns a business in motor vehicles. He says the buying power(independent variable) of people controls our sellings(dependent variable), but on a specific occasion like on Eid night (Chand rat ), there is thrust in our business. So here, this specific occasion can be the extraneous variable which affects the profit.
🔹️Algebraic expression:
A+B= C
A=independent variable ( buying power)
B extraneous variable (a specific occasion)
Dependent variable (results in terms of car sails)
🔷️Intervening variables
This is a concept which explains how an independent variable affects the dependent variable. It is a connection between dependent and independent variables.
🔹️Practical life example:
While studying the impact of light on the production of food in plants the photosynthetic process is an intervening variable explains that how light controls food production( i.e food is in the form of carbohydrates)
🔹️Algebraic expression
C= F+D
C=dependent variable (plant food production)
F=independent variable( light)
D=intervening variable (photosynthesis)
Algebraic expressions consist of constants (mostly numerics), variables and algebraic operations (like subtraction, addition, multiplication etc.). Expressions are algebraic statements which are translations of theory to solve mathematical problems
➡️Example
2m^2 -5n + 3
In the above expression, the first term includes a constant number 2, a variable m, and an exponential power of 2 for the variable m. The second term is a negative one and has a coefficient and a variable. The last term is just a positive number
Types of expression
🔷️Rational expression
This kind of expression includes fractions along with variables, constants and algebraic operations.
🔹️Practical life example and its algebraic representation
Here in Sargodha, we have a lot of kino or mandarin fields. So it helps me to extract a real-life example for rational expressions. To calculate the expense of a single sapling cultivation we can proceed as follows
In an acre, if there are x number of plants ( here, plant number is taken as x because the number could be varied depending on the condition of the soil and desired distance between the plants). And a single sapling costs Rs250. Now the further expenditure of fertilizer is about Rs20000 for an acre. So, to calculate the cost of one plant, we can use follow rational expression.
(20000+250x) / x = cost of single plant cultivation
In the above expression, we add the fertilizer cost to the total expense of all the saplings and then divide it by the total number of plants.
🔷️Polynomial expression
A polynomial expression contains one or more than one algebraic term. These terms are combined with mathematical operations except division.
There are some conditions which must be fulfilled for a polynomial expression
The power of variables and exponents must be positive
Variables shouldn't be in non-polynomial functions or in denominators
🔹️Real-life example and its algebraic representation
If we have to calculate the profit from one acre kino field for 1st year of production we have to include various variables given as follows
w=cost fuel for tractors
250x= cost of plants
y=irrigation, fertilizers expenditure
z= labour cost
So the algebraic expression for total profit at which field is sold can be written as follows
A - ( w+ 250x +y +z)= total profit
Here, I subtract all the expenditures ( except the land rent, which can be included if someone doesn't own it) from the cost at which a fruit of the field is sold.

Task # 2 |
|---|
Show your way of evaluating of an algebraic expression if values of variables are given? Step by step explanation required!
The algebraic expression which I'm going to simplify is given as follows
4a + 3b^2 - c ...(i)
The values of variables are as follows
a= 5
b=2
c=10
To start the simplification of this expression put the values of variables in their respective places in (i)
So the expression becomes as
4×5 + 3×2^2- 10 ...(ii)
According to the PEMDAS rule exponents are first to be solved so in this expression two raised to the power two is simplified as
2^2 = 2×2 = 4
putting the 4 into ...(ii) we gotthe expression as
4×5 + 3×4 - 10 ...(iii)
We solve exponents according to PEMDAS because parentheses are not present in our expression.
In this step, I solve the multiplication as follows
4×5 = 20
3×4 = 12
By putting the multiplication values in ... (iii) we got the following expression
20 + 12 - 10 ...(iv)
In this step, addition is performed according to the order of solution as follows
20 + 12 = 22
By placing this value in .... (iv) we got
22 - 10 ...(v)
In the last step, we simply substrates 10 from 22get and got our final answer
22- 10 = 12 ...(vi)
Final answer
So here " 12" is the answer as a result of the simplification of the expression (i)
 |
|---|
Handwritten to avoid any ambiguity.

Task # 3 |
|---|
Solve the given algebraic expressions
Expression #1
Simplify the expression : 3(2x - 1) + 2(x + 4) - 5
In the first step on multiplication or distribution of 3 with the terms present in 1st parentheses, we got the expression as follows
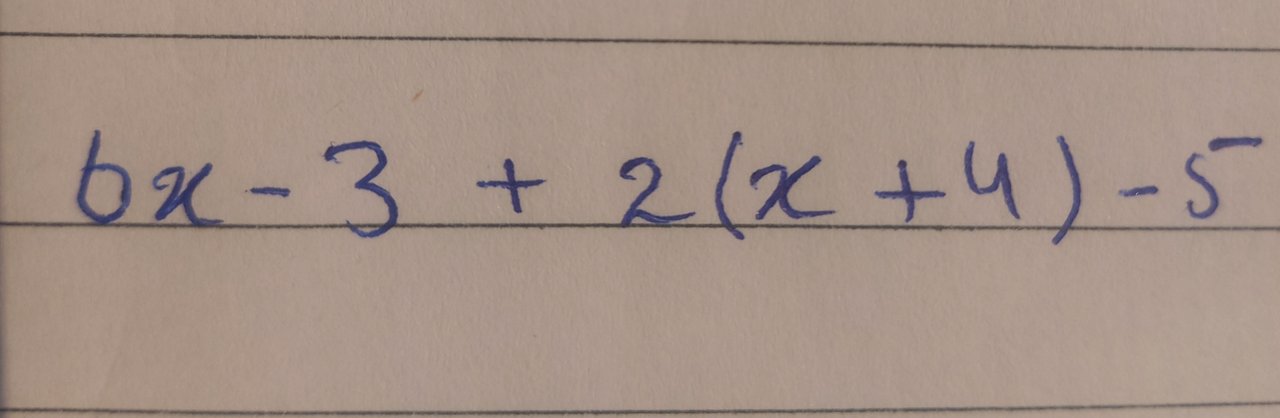
In the second step, I multiplied 2 with the second parentheses which left us with a linear expression given below
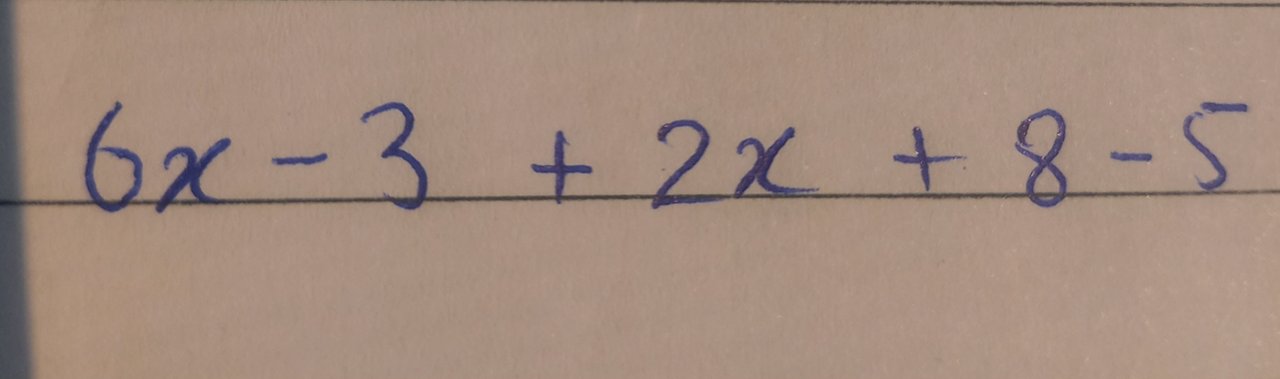
In third step, I rearrange the expression to gather the like terms
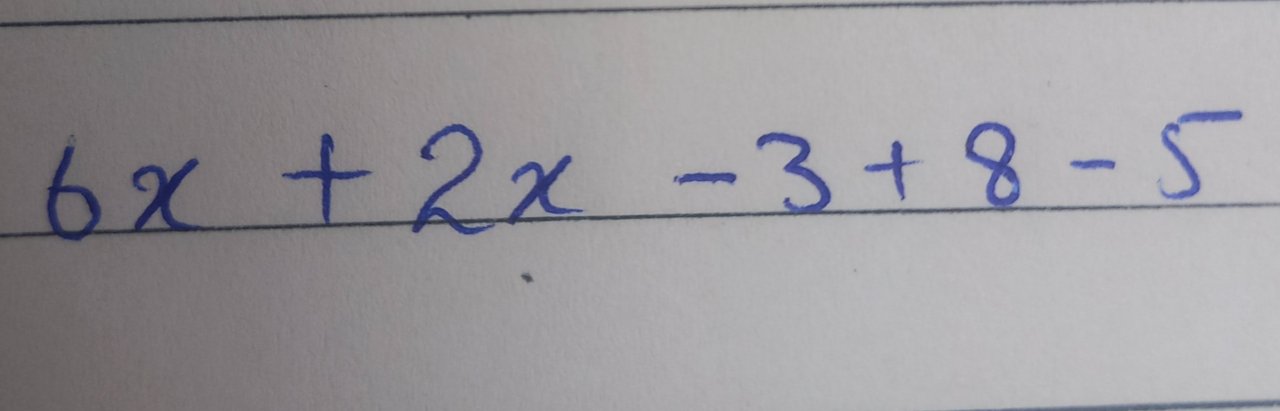
By performing addition and subtraction respectively we get
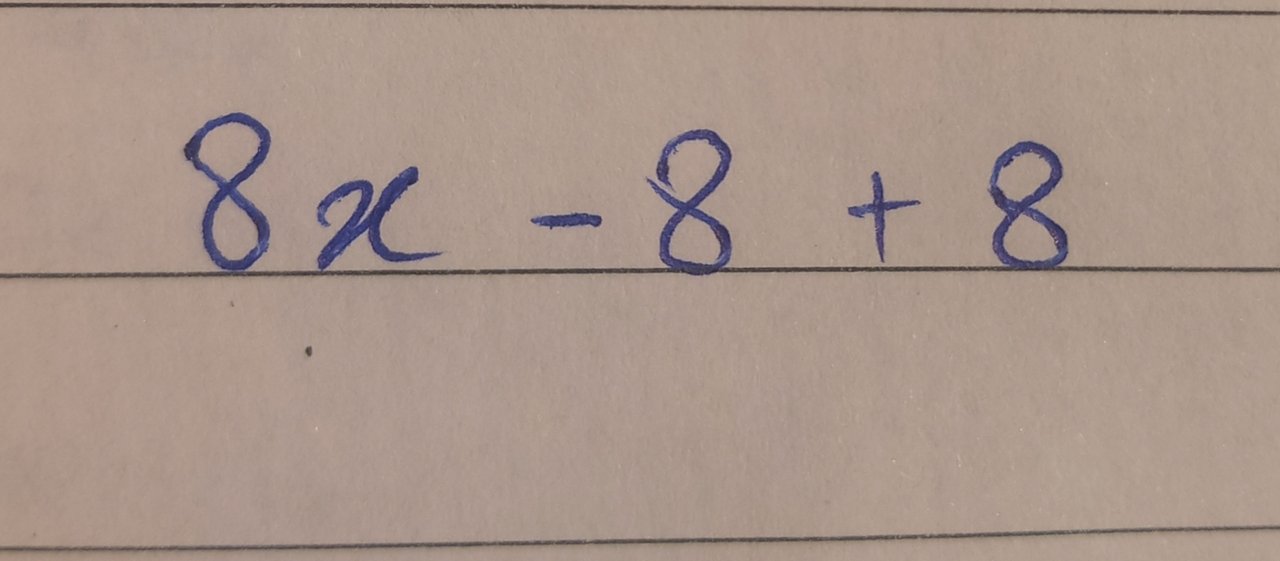
8x
The final answer is 8x which is obtained when the negative eight is sub substrated from plus eight

Solution of expressions 2, 3 and Task 4 is posted in comments section.
Thanks to @khursheedanwar for being cooperative and helping to handle such a complex topic in an effective
@aliraza51214 , @sojib1996, @aminasafdar and @iqrabatool34 would you like to crack algebra.

Comments