"SLC-S22W1/Variables and Expressions"
6 comments

•Tarea 1
En esta oportunidad hablaré de dos tipos de variables que son, variables discretas y continuas:
- Variables discretas: son aquellas en la que solo toma números finitos, es decir, los valores se obtienen contando, estas variables no suelen tener números decimales. Por ejemplo, podemos contar la cantidad de colores que tenemos, porque pueden ser 4,6,9,10.
Otro ejemplo es la cantidad de libros que puede haber en una librería o biblioteca, solo necesitamos contar para poder determinar la cantidad.
- Variables continuas: a diferencia de las variables discretas esta toma números infinitos, es decir, los valores se obtienen midiendo y suelen tener números decimales. Por ejemplo, una persona puede medir 1,55 metros o también podría ser 1.70345 metros no hay un valor exacto en la altura de una persona.
Ahora, las expresiones pueden varias según como estén estructuradas, estas pueden estar combinadas de números, letras, signos.
- Expresiones exponenciales: son aquellas que tienen la variable en el exponente de una base, por ejemplo,
4^x=2
6^(4x)= 12
- Expresiones radicales: son aquellas expresiones que tienen una raíz, ya sea raíz cuadrada, raíz cúbica, etc, por ejemplo.
Aquí tenemos una raíz cuadrada con el número 5 y el exponente 4
√5^4
Resolviendo quedaría, sacamos el 5 de la raíz, luego dejamos el exponente pero dividimos entre 2 porque la raíz es cuadrada.
5^4/2
Dividimos el exponente
5^2
Ahora multiplicamos, resultado 25
•Tarea 2
Teniendo la expresión a evaluar que es:
3X+4Y^2
Los valores de las variables son; X=2 y Y=3

Ahora sustituimos los valores en el lugar de cada una de las variables
3(2)+4(3)^2
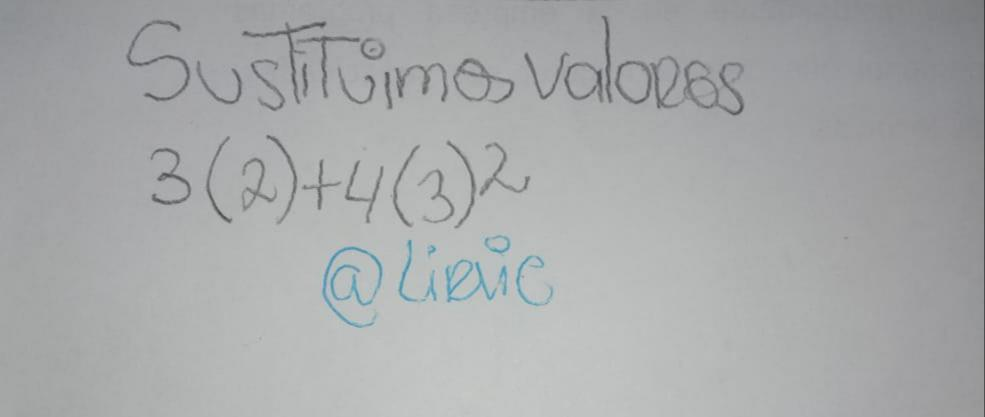
Luego multiplicamos tanto el producto como el número que tiene el exponente.
6+4(9)
6+36
Para finalizar realizamos la última operación que tiene la expresión, es decir, sumamos:
42

•Tarea 3
Lo primero que hacemos es distribuir los número que multiplican a los paréntesis
3(2x - 1)= 6x-3
2(x + 4)= 2x-8
Ahora, con la siguiente expresión agrupamos términos semejantes quedando;
6x-3+2x+8-5
6x+2x+(-3+8-5)
Realizamos las sumas y restas correspondientes,
8x + 0 = 8x


Lo primero que se debe hacer es sustituir la X por 2, luego es muy sencillo solo realizamos las operaciones correspondientes sumamos y restamos lo que esta en el numerador, luego dividimos dando como resultado 5÷3 es igual a 1,6.
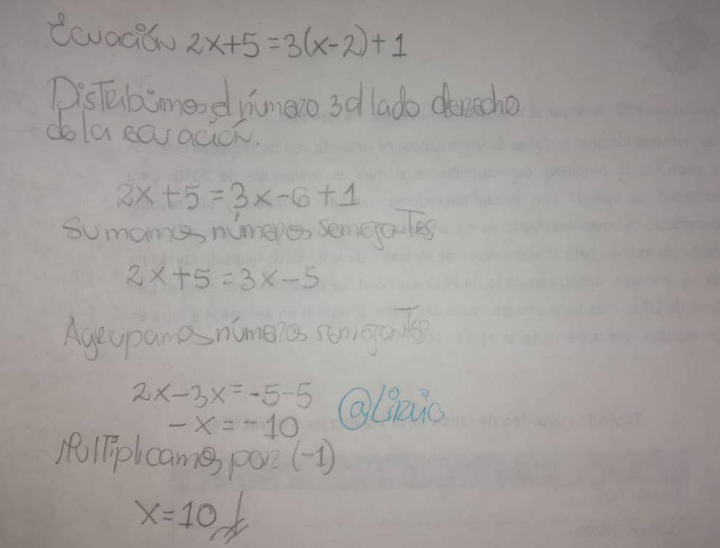
Distribuimos el número 3 en el lado derecho de la ecuación, luego sumamos números semejantes, seguidamente procedemos a despejar X, de lado izquierdo colocamos los números con X y de lado derecho los números que están sin X, hacemos las sumas y restas correspondientes, como el resultado que obtenemos es negativo para eliminarlo multiplicamos por -1.
•Tarea 4
• Supongamos que hay una panadería que vende un total de 250 panes al día. Se venden panes de trigo integral y pan blanco, y la cantidad de panes de trigo integral vendidos es 30 veces mayor que la cantidad de panes de pan blanco. Si x representa la cantidad de panes de pan blanco vendidos y la panadería obtiene una ganancia de $0,50 por cada pan blanco y $0,75 por cada pan de trigo integral, escriba una expresión que represente la ganancia diaria total de la panadería.
Se venden un total de 250 panes.
X representa el número de panes blancos vendidos, como la cantidad de panes de trigo es 30 veces mayor entonces se representa x+30 quedando la siguiente expresión;
x+(x+30)=250
Sumamos términos semejantes
2x+30=250
Ahora, para despejar x restamos 30 en ambos lados de la ecuacion quedando de la siguiente forma
2x=220
Despejamos X
X=220 / 2 Dividimos
Resultado X=110.
Quiere que la cantidad de panes blancos vendidos son 110 panes, y como la cantidad de pan integral es 30 veces mayor sumamos 110+30=140, este es el total de pan integral vendido.
Para determinar las ganancias:
Ganancias de pan blanco $0,50
Ganancia de pan integral $0,75
Queda la siguiente expresión:
Ganancia total: (0,50x)+(0.75(x+30))
Sustituimos los valores: 0,50x+0,75x+0,75(30)
Sumamos los valores que están con X
1,25X+0,75 (30)
Ahora multiplicamos para eliminar paréntesis.
Ganancia total= 1,25X+22,5
• Supongamos que el costo de alquilar un automóvil por un día se representa mediante la expresión 2x + 15 y donde x es el número de horas en las que se alquila el automóvil. Si la empresa de alquiler ofrece un paquete de 3x - 2 dólares para los clientes que alquilan el automóvil durante más de 4 horas, escriba una expresión para el costo total de alquilar el automóvil durante x horas y muestre cómo la simplifica.
Costo de alquilar un automóvil por día 2x+15
Paquete ofrecido a los clientes durante más de 4 horas
3x-2
Costo total= (2x+15)+(3x-2)
Ahora quitamos los paréntesis y agrupamos los números que están con la X y los números que están sin X.
2x+3x+15-2
Resolvemos la operación realizando una simple suma y resta, donde el costo total quedaría de la siguiente manera.
Costo total 5x+13
Invitó a participar a
@jimiaera02
@alee75
@sahar78
Imágenes propias tomadas con mi teléfono redmi 10 la de portada editada en canva
Si quieren conocer más de mí los invito a visitarme: https://steemit.com/hive-172186/@lirvic/mi-presentacion-en-steemit-y-mi-logro-1

Comments