SEC-S20W5 Iteration in Programming: For, While, and Do-While Loops

Hello Steemians, welcome to my post and stay safe as you read through this post.

---

Edited with canvas

---

1⳾ Why are loops necessary in programming? Which type of loop did you like the most?

In programming loops are necessary as they allow us to repeat a block of code multiple times, making our program reducing redundancy and more efficient. Without loops, it wouldn't be possible for us to manually repeat code for each iteration, which could be error-prone when we are dealing with numerous tasks. This means that loops are ideal for tasks like iterating through the data structure, managing dynamic conditions, and automating repetitive tasks.

---

Types of Loop

There are three types of loops that I know about and it is for loop that I like the most. Before we get to know the reason why It's my type of loop let's briefly look at the types of loops first.

• For loop:
  This is the type of loop that is been used when the number of iterations is known in advance.

• While loop:
  This is the type of loop that is been used when the number of iterations is not known, and the loop runs as long as a condition is true.

• Do-While Loop:
  This is the type of loop that is similar to that of the while loop, but it ensures that the loop runs at least once, and since the condition is checked after the first iteration.

The reason why the for loop is my preferred type of loop is because it is a loop that is concise and easy to control when iterating over lists, known ranges, or arrays. Also, it is a straightforward loop and prevents potential infinite loops that are most likely common with a while loop. In a simple word, it is the simplest, easy, and understandable loop.

---

2⳾In task #8 from the last lesson, the condition for determining if buildings are on the same side of the street should have been written as if(n%2 == m%2)instead of: if(n%2==0 && m%2==0 || n%2==1 && m%2==1) Explain both conditions in words. Which one is better and why?

Both conditions are tailored to check whether two buildings, numbered n and m, are on the same side of the street. Below is an explanation of the both conditions.

• Condition 1: if(n % 2 == 0 && m % 2 == 0 || n % 2 == 1 && m % 2 == 1)

The above condition checks if both numbers are either odd or even: n % 2 == 0 && m % 2 == 0: This checks if both numbers are even. If both are divisible by 2 with no remainder, they are on the same side. n % 2 == 1 && m % 2 == 1: This helps to check if both numbers are odd. If both leave a remainder of 1 when divided by 2, they are also on the same side.

Since it uses two different (seperate) conditions: one is for both being odd and one for being even.

• Condition 2: if(n % 2 == m % 2)

The above condition is a condition that directly compares the remainders when both n and m are divided by 2: if n % 2 equals m % 2, then both n and m are either both odd or even number, meaning they are on the same side.

---

The Better One and Why

It is the Condition 2: if(n % 2 == m % 2) that is better based on the following reasons of mine.

• It is the condition that is easier to read. The logic is clearer, as it directly compares the remainders rather than needing to break the conditions into two different parts.

• It is the condition that is more concise since it combines the check for both odd and even numbers into one simple comparison.

• The condition is more efficient as it avoids the redundancy of checking two different conditions and simplifies the logic to a single operation.

---

3⳾Output the number 33 exactly 33 times using each type of loop.

Here, I have shared how we can output the number 33 exactly 33 times using each type of loop. Here, we will be using Python programming language to see how everything can be done.

Using a for loop:

for i in range(33):
    print(33)

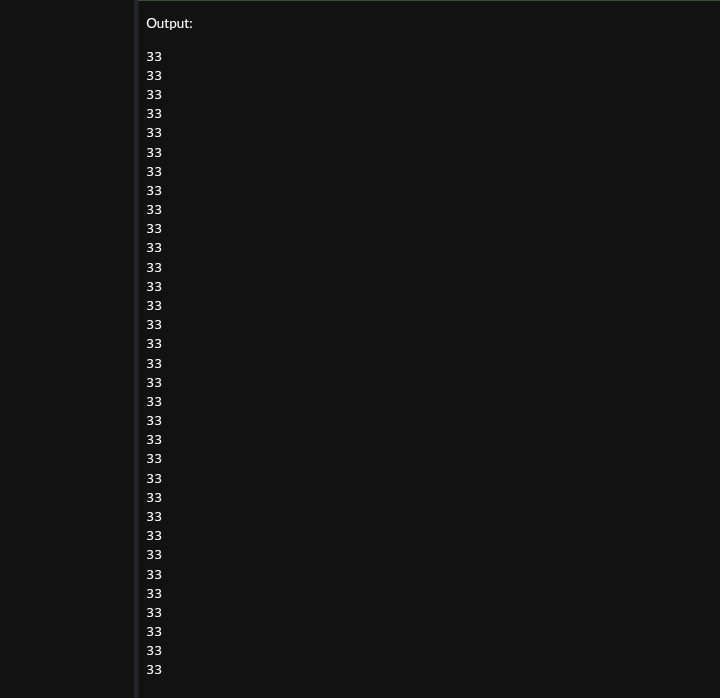
Using a while loop

i = 0
while i < 33:
    print(33)
    i += 1

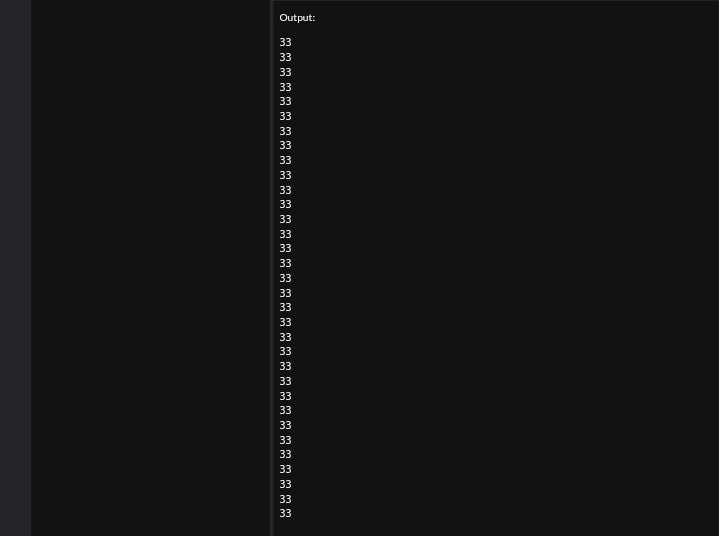
Using a Do-While Loop

i = 0
while True:
    print(33)
    i += 1
    if i >= 33:
        break

Each of the above, given loops will print the number 33 exactly 33 times. The first is the for loop concise when we know the number of iterations before time. The while loop which is the second gives more flexibility for dynamic conditions, whereas the do-while loop which is the third, makes sure that at least one iteration, is respective of the condition.

---

4⳾Output numbers from 11 to 111: 11, 21, 31... 101, 111, but skip the number 51 (using one type of loop). (Tasks 1-4: 1 point)

Here, I have shown an example of using a for loop to output numbers from 11 to 112, skipping the number 51:

for i in range(11, 112, 10):
    if i == 51:
        continue
    print(i)

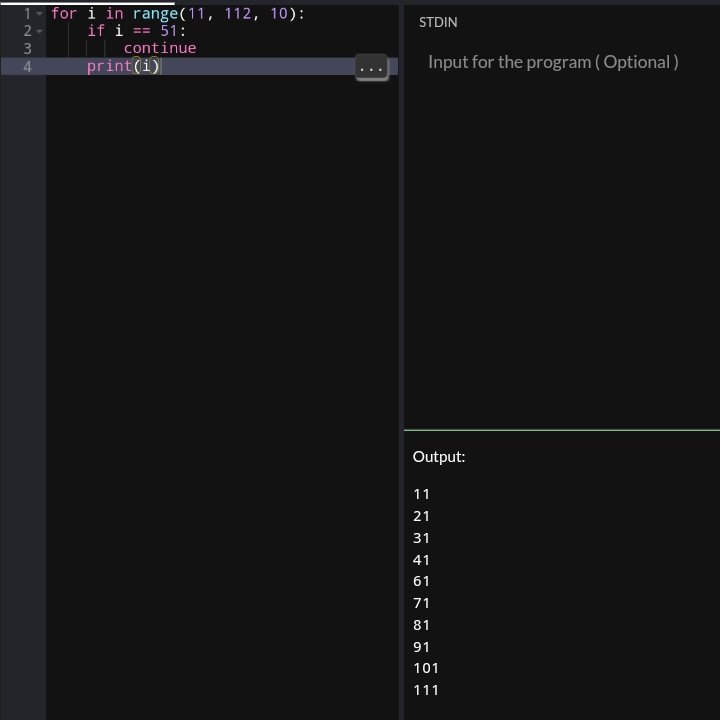
Interpretation

• The range(11, 112, 10) generates numbers starting from 11 and increased by 10 up to buy not including 112.

• The if I == 51: continue skips the number 51 when encountered (being faced).

---

5⳾Output the multiplication table for a random number, for example, for 0:

Here, I have shown how to output the multiplication table for a random number, for example, 0 which you can see as shared below.

num = 0  # Replace with any number for a different table
for i in range(1, 11):
    print(f"{i} x {num} = {i * num}")

---

For example, if I set num = 0, it will generate as shown below.

Also, if I change the num value, I will get the multiplication table for the number.

---

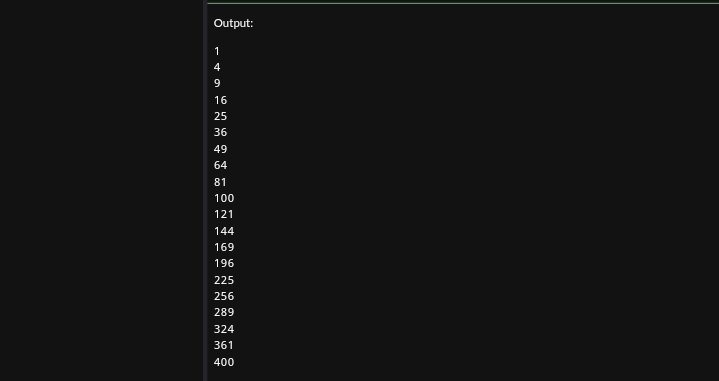
6⳾Output the squares of numbers: 1, 4, 9, 16, 25, 36, 49... 400.

Here I have shown how we can output the squares of numbers from 1, 4, 9, 16, 25, 36, 49... 400.

for i in range(1, 21):  # 20^2 = 400, so we go from 1 to 20
    print(i * i)

The above code will generate the output shown below.

---

7⳾Output the powers of some number: 1, 2, 4, 8, 16, 32, 64, 128... less than 3000.

Here, I have shown how we can output the powers of a number example powers of 2 that are less than 3000:

num = 2  # Replace with any base number
power = 1

while power < 3000:
    print(power)
    power *= num

For powers of 2, the output will be as shown below.

We can change the num to any other base number to get powers of a different number.

---

8⳾How many even four-digit numbers are there that are not divisible by 3? (Tasks 5-8: 1.5 points)

For us to determine how many even four-digit numbers are there that are not divisible by 3, we will have to follow the steps below to know the now many they're.

• Step 1: We need to first calculate the total number of even four-digit numbers.

• The range of four-digit numbers from 1000 to 9999

• For a number to be even, the last digit must be one of (0, 2, 4, 6, 8).

• Step 2: At this step we need to get the total number of even four-digit numbers:

• The first digit **thousands place can be any digit from 1 to 9, option 9.

• The second and third digits can reach any digit from 0 to 9, option 10.

• The last digit unit place must be one of **0, 2, 4, 6, 8 options 5.

However, the total number of even four-digit numbers is

9 × 10 × 10 × 5 = 4500

• Step 3: We have to determine how many of these are divisible by 3

• A number is divisible by 3 if the sum of its digits is divisible by 3.

• For simplicity, we can calculate how many four-digit even numbers are divisible by 3, and then subtract (minus) it from the total.

Even number divisible by 3:

• Since we don't have an easy formula that gives this count we will have to try modular arithmetic for each case, so we can skip directly to using statistical rules.
• About one-third of the numbers are divisible by 3.

4500/3 = 1500

Step 4: We will have to calculate how many are not divisible by 3.

• Substract (minus) the number of even four-digit numbers divisible by 3 from the total number of even four-digit numbers.

4500 - 1500 = 3000

From above it means there are 3000 even four-digit numbers that are not divisible by 3.

---

I am inviting: @kuoba01, @simonnwigwe, and @ruthjoe

Cc:-
@sergeyk