SLC S22W1 : Variables and Expressions
2 comments

Most people are scared of studying mathematics because they feel they won't be good enough or that failure may be a backbone in their journey. Why? This is probably because of how the mathematics is being taught or probably from the interest of the student. The teacher plays an essential part in making students hate mathematics as a course. The complexity involved makes it a weird subject by most and they flee to something simple.
Now, this post is talking about Variables and Expressions which seems to be the basics when it comes to algebraic expression. Without accurate knowledge of these two terms, it must be difficult to navigate your way through algebraic except doing so blindly. In the course of this post, I'll be breaking things down using the tasks involved for a lay man to understand and those that have little or no interest in mathematics.
Before mentioning the two types of variables and expressions not mentioned in the tutorial post, I'll love to shed more light on these two terms. Let's take this illustration. It's more like you're baking a bread in a bakery. You'll definitely need a recipe of 2 cups of flour or more, 1 cup of sugar and a temperature. The amount of flour and sugar varies depending on the number of baked bread but the temperature is constant.
Variables are symbols or components that represent a value which can vary and are just like the measurements or amount of ingredients that can change. In terms of expressions, it's likened to the instructions in the recipe used to make the bread. It doesn't represent set of letters alone but is a combination of numbers, variables, constants, and operations that gives you an outcome just as you combine the flour and sugar with the instructions in the recipe to make the bread.
Why it's called instructions in the recipe is because you'll add, add and add or subtract, add and subtract.
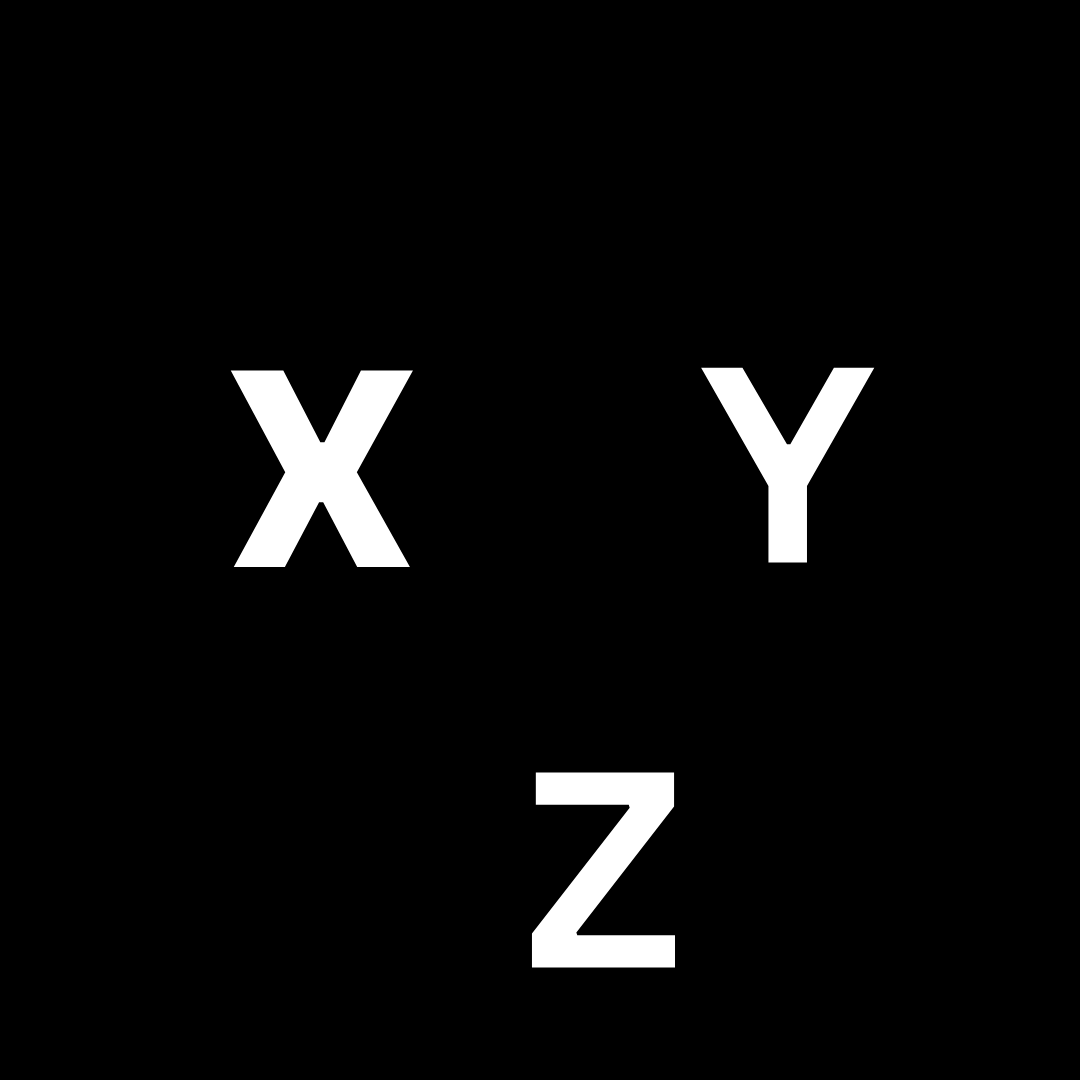 | 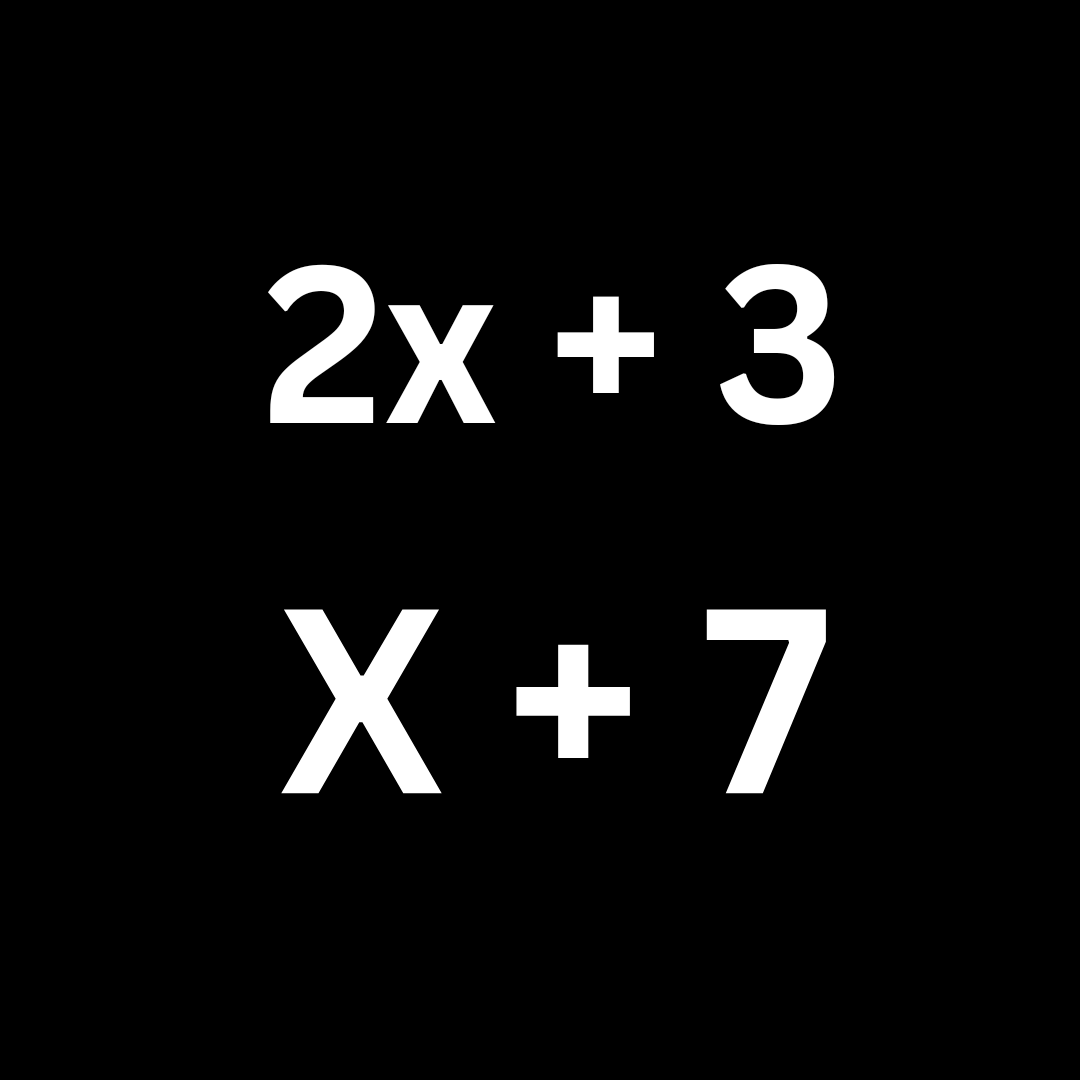 |
|---|
X - Variable
2x - Dependent Variable
2x + 3..... Expression
Explain 2 variables and expressions types other than that which are explained in this course.(Practical and algebric examples are required!) |
|---|
We have different types of variables which can be extended to other course of study, research etc. I'll be focusing on two types of variables which are mathematically related. Constant Discrete Variable.
- Constant Variable: A constant variable is a mathematical variable and mostly used experimentally in other field. It's a variable whose value does not change under conditions that are specified. Unlike other variables that can change, constant variable as the name implies is fixed and provides stability in calculations. How constant is this variable?
Let's take these examples. Constants as we know serves as parameters used in solving equations and ensuring calculations are consistent with themselves. We have seen constant variables as such in experimentations like physics. Some constant variables are;
g= 9.8m/s², plank's constant, c= 3×10⁸m/s...etc.
Even in real life, we have constant values in terms of the price of an item in a closed market where you don't get to price it. Mathematically, we can show this constant variable in linear equations.
y = mx + c
C there serves to be the constant value most especially when plotting graphs. In quadratic equations, we have
y = ax² + bx + c.....
- A discrete variable is mathematically related and is one that has specific counting when applied and there are values in between values like decimal or fractions as the case may be. They are values that are distinct and separate from each other, mostly appearing as whole numbers.
What I mean here is that, discrete variables are usually represented when counting but the counts involves distinct whole numbers. E.g in algebraic expressions, the number of free spaces can be calculated as F = 50 - n where n can be any number or discrete variable.
Same is applied when given as expression that involves n days. We could write it as
P= p¹ +p² + ........+ Pn
The practical application of this is when you're reminded that discrete variables can only be counted with specific values. They can't be measured as it's done in continuous variables. It's more like comparing the speed of a car and the number of balls in a house. The speed of a car can only be measured while that of the balls can be counted with specific values which can be extended to what we call n values in physics.
Having considered variables and their Practical applications, let's look into Expressions carefully and how they are applied. I'll be emphasising on two types of expressions which includes Polynomial and Rational Expressions
Expressions |
|---|
- Polynomial Expressions are expressions that consists of variables raised to non-negative integer powers, constant and coefficients. What do I mean? This expression involves a variable being raised to the power of an integer that doesn't have a negative symbol attached to it. Let's take this example in physics where we have to use the laws of motion to explain this, practically.
Let's assume we are given an expression such as this and are asked to identify what kind of expression this is.
h(t) = 5t² + 20t + 6
In this expression, we can easily denote a physics expression which signifies projectiles and that's how this polynomial expression is linked, practically.
Mathematically, using the algebraic example, we can outrightly identify a polynomial from its power. Polynomials usually have variables raised to the power of 3 or more while quadratic is 2. .
Example: 3x³ - 6x² + 2x + 6
In this case, this is an expression but when an equality sign is introduced, it becomes an equation.
3x³ - 6x² + 2x + 6 = 0....... Equation
- Exponential Expressions: This could be more tempting as one may feel it's a dependent variable but it's not. The variable at the superscript represent power. An exponential expression involves variables or constant, raised to the power where the exponent is a variable.
How? The exponent here is the variable and this variable is the raised power of a base. Practically, we've had series of formulas with exponential expressions as
P(t) = P°Ert
We usually see it used in calculating the population of a place and mathematically, and we usually come across expressions such as
3^x . 3²x ÷ 3²x+¹
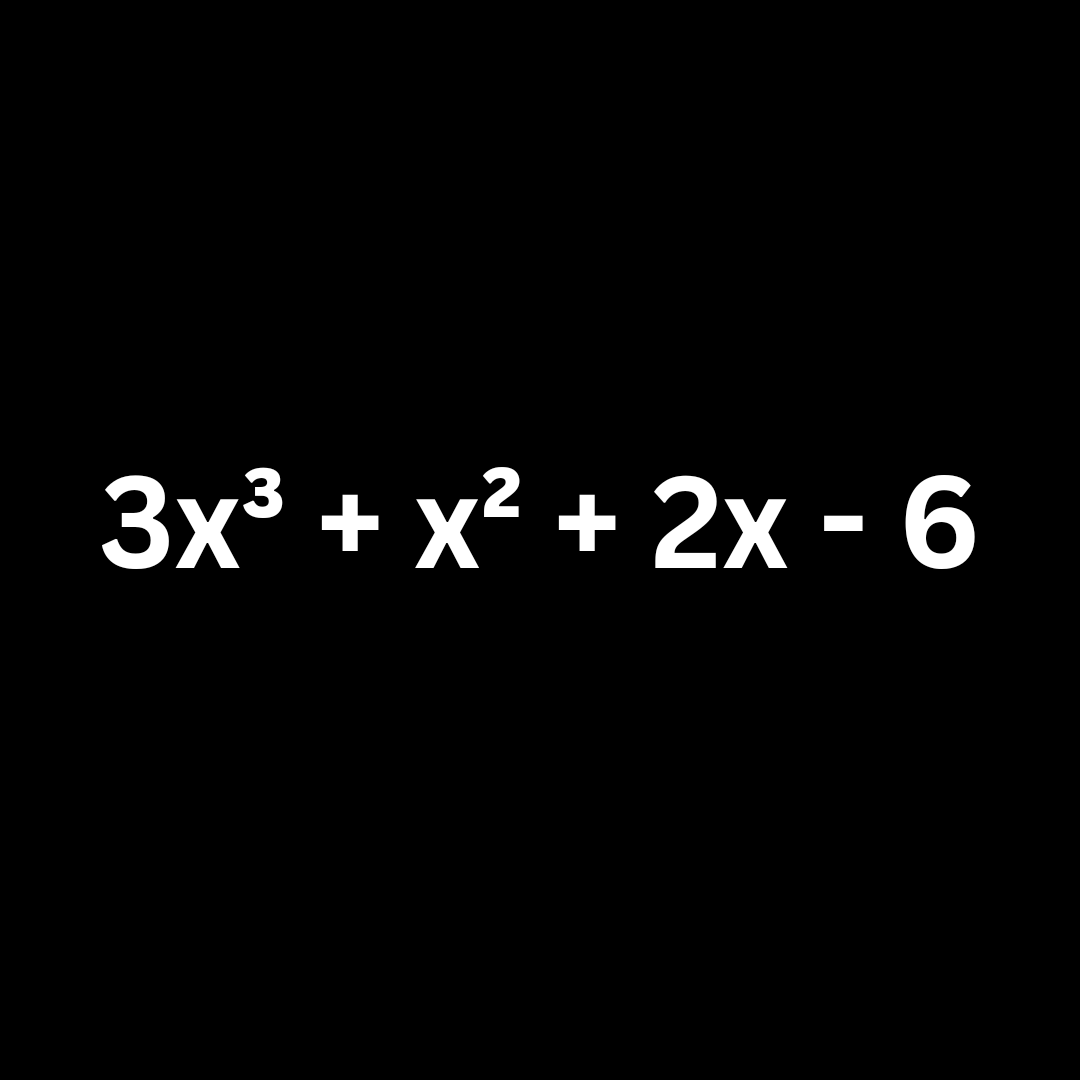 Polynomial Polynomial | 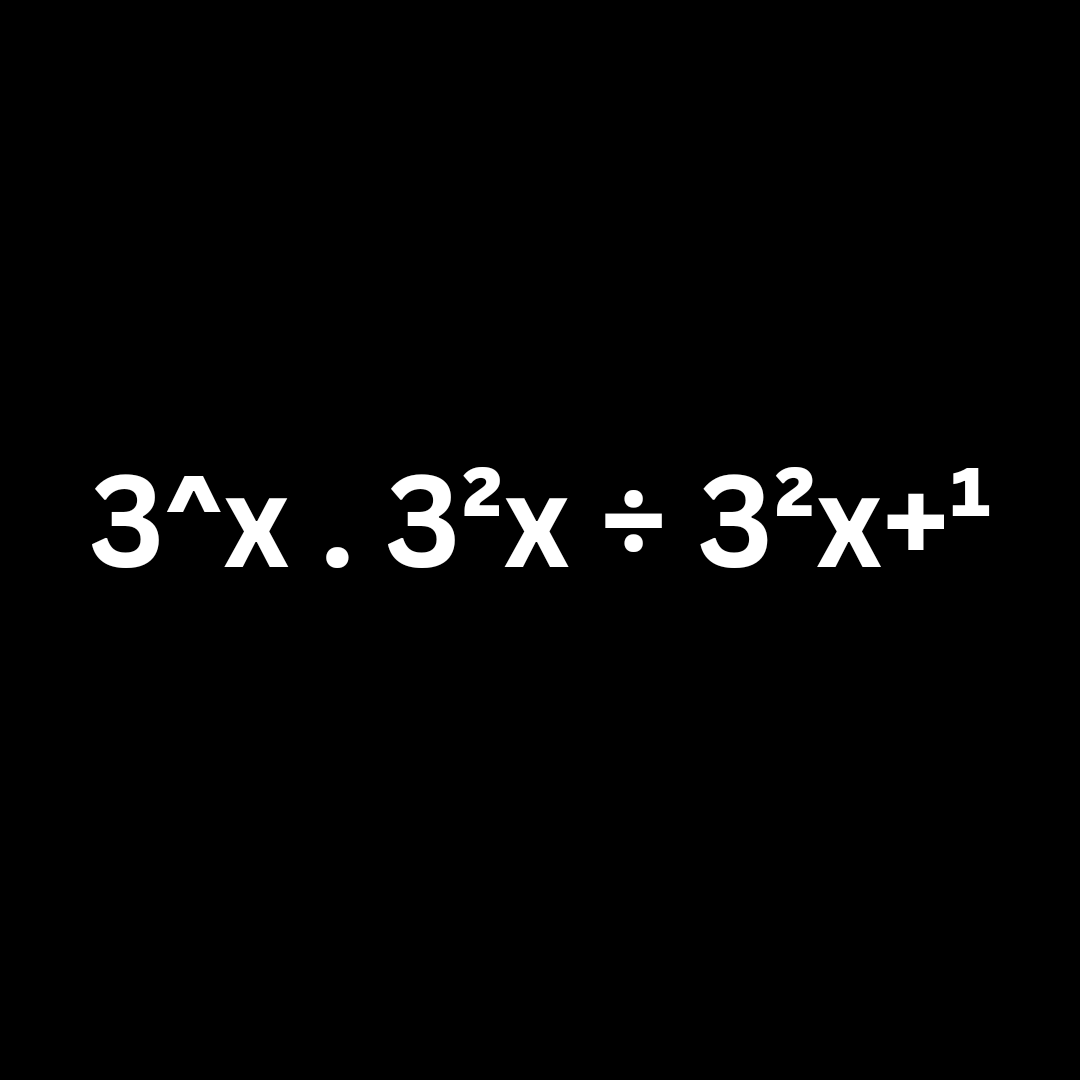 Exponential Exponential |
|---|
Variables and Expressions are closely related and we use them in day-to-day activities. Both can do without each other and can become independent of themselves.
Task 2 |
|---|
Evaluating an algebraic expression is just like unlocking a secret code. You need to be accurate in where you touch first otherwise you'll have to retry after 24 hours. There are rules governing how algebraic expressions behave. You don't just see these expressions and start working on them without understanding the logic and mathematical rules involved.
In my primary school, I was taught BODMAS. This was and is still used in this century to solve most mathematical problems. The rule is as simple as the structure of the house. You can't enter a house through the window without first passing through the door. You can't enter your room without going to the lobby area first, where your room is stationed.

Same applies in mathematics. You can't count 2 when you haven't counted 1. So let's understand what the letters represent first before venturing into the practical application of what I'm saying.
B - Bracket: In most algebraic expressions, you get to see brackets covering variables and you're expected to open these brackets but how? Do you carry key to open the brackets? Definitely not. This brackets are the priorities in BODMAS. It usually in the form of parentheses. These brackets usually mean multiplication in cases where you have a number in front of the bracket with a sign.
Example: (3+5) = 8
2 ( 3+5) = 16✅
You'll open the brackets by solving what's inside before opening it. This is done irrespective of the signs involved. Once you open the brackets, the integers or variables stand on its own and from there, you can be able to solve them as like terms or distinct terms as the case may be.
O - Order This means exponents or powers usually seen in some equations. These exponents as mentioned earlier under exponential expressions are powers like squares, cubes, and any other powers which may range into polynomial. These exponents are usually at the superscript of an integer or variable variable and can be numbers or letters. In some cases, they are found raised at the top of a bracket which needs to be open first before touching the parenthesis
Example: 2² + 4 = 4 + 4 = 8
(3-2)² ÷ 1 = (1)² ÷ 1 = 1✅
D - DIVISION: As the name implies, this have to do with the division of numbers, variables etc in the expression. When this division is done as the third rule after opening the brackets, multiplication would be introduced as the fourth rule that governs our operation in algebraic.
Example: 15÷5 = 3
(5+3) ÷ 2 = 8 ÷ 2 = 4✅
M - MULTIPLICATION: This is actually the next rule after the division rule. It follows a sequence and after the division aspect comes the division. It is usually represented with the symbol. X
Example: 3×5÷5 = 3 × 1 = 3
8 × 2 = 16✅
A - ADDITION: This is simply the addition of numbers and letters in an expression. The symbol used to denote this is the + sign. Mathematically, we open brackets, divide and multiply before we add and then subtract which is denoted by the symbol -
Example: 6+3-1
9-1
8 ✅
S - SUBTRACTION: This is a BODMAS RULE that involves subtracting integers and variables which could be independent and dependent.
Now let's put everything together in an application. Let's imagine we've been given an algebraic expression.
Evaluate 2 - 5(3+4) + 25 ÷ 5 - (3×6) using BODMAS rule
Evaluate 4 + (12÷3)² × 2
Solution |
|---|
We outrightly know that the above is an expression and not an equation. If you notice in the expression, we have brackets, division, exponent, multiplication and addition. You should take note of what you have in the expression first before venturing to something else.
Step 1: 4 + (12÷3)² × 2
Open Brackets:
4 + (4)³ × 2
Step 2: We would work on the Order or exponent that's after solving the brackets.
4 + (4 × 4 ) × 2
4 + 16 × 2.............
After solving the exponent and getting a plain exponent, we have to still use the rule because if we want to punch our calculators, we would get a different answer.
Step 3: Multiplication comes first before addition as shown in the expression. Now let's multiply 16 by 2 in the expression.
4 + 16 × 2......
4 + 32 ........ Multiplication
Step 4: We then add to get our final answer as simple as it could be. Now, for something complex, I'll be showing you via video.
36.... We've gotten our final answer for the expression.
| Therefore, 4 + (4)² × 2 = 36 ✅ |  |
|---|
🔴 Example 2: Evaluate 2 - 5(3+4) + 25 ÷ 5 - (3×6) using BODMAS rule
Step 1: Brackets got us. We'll solve the bracket first before doing any other operation.
2 - 5(3+4) + 25 ÷ 5 - (3×6)
B - Brackets
(3+4) and (3×6)
(7) and (18).....Then let's place these values in their respective positions........
2 - 5(7) + 25 ÷ 5 - (18)
Now if you're not careful, you'll make a big mistake in the brackets that are still available. One bracket has a number close to it and another has a sigb close to it. What do we do, we use what's in front of the bracket and multiply what's inside the bracket to open it. Remember, bracket is otherwise called multiply, that's only when there's an integer in front of the bracket.
2 - 5(7) + 25 ÷ 5 - (18).....
2 - 5×7 + 25 ÷ 5 - 18.....
2 - 35 + 25 ÷ 5 - 18......
Step 2
We're done removing the brackets, next thing is the exponent which we don't have in the expression. So we'll move to Division.
We have 25 ÷ 5 = 5
Which is 5. Replacing it in its position, we have .....
2 - 35 + 5 - 18......
Step 3
We are reducing this expression gradually. The next thing is multiplication after division. So we have no multiplication sign there. We move to Addition and then subtraction.
2 - 35 + 5 - 18.......
-35 + 5....... - 30
We'll replace the - 30 in the position where we have - 35 +5
2 - 30 - 18 ........ - 46 ✅ which is the answer to our algebraic expression....
 | Answer |
|---|
We won't be using the same rule in solving task 3 though it would be a little bit complex. It would just need some manipulation and I'll show you how to do this easily without making it difficult to understand.
- Simplify this expression: 3(2x - 1) + 2(x + 4) - 5
Solution |
|---|
This expression is similar to the one I solved earlier before now. So the first rule we'll apply is the opening of Brackets as there are some brackets here......
3(2x - 1) + 2(x + 4) - 5
Step 1:
Open the brackets.......We don't have any like terms in the brackets to solve. We have two unlike terms of which one is with a letter and the other is just a number. How do we open the brackets? By multiplying what's inside the brackets with what's outside.
Let's break it down......
3(2x-1)
3 would be used to multiply 2x and 1 as 2x and 1 aren't like terms.
3 × 2x = 6x
3 × 1 = 3
So we have 6x -3.........1
Now, the second bracket is 2(x +4 )
2 would be used to multiply x and 4 as x and 4 aren't like terms.
2 × x= 2x
+ 2 × 4 = 8
Now, we still have our positive sign as positive plus positive is positive.
2x + 8.............2
Substituting the values, we have..
6x -3 + 2x + 8 - 5......
This is the expression we've arrived at after opening the brackets. In this case, we'll have to collect like terms . Take the x to one side and the integers to the other side. In this case since we aren't dealing with like terms, the BODMAS principle won't come in.
6x will take +2x to itself on the left while - 3 + 8 - 5 will go to the right.
6x + 2x - 3 + 8 - 5.....
6x + 2x....8x
-3 + 8 - 5....0
| We have 8x + 0.....Since anything added or subtracted by zero is that thing, we have 8x as the answer. |  |
|---|

Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2 |
|---|
(X² + 2x - 3) / (X + 1) when x = 2
In this, we have a quadratic expression and a linear expression. We also have a factor where 2 is the function of x. f(x) We'll start with the quadratic expression.
f(x) = (X² + 2X - 3)
Since 2 is a function of x, we'll be substituting 2 with x in the expression.
f(2) = (2)² + 2(2) - 3...........1
4 + 4 - 3.....
8 - 3 = 5.......1
For the second expression, (x + 1), we'll substitute 2 for x to get an integer.
f(x) = (x + 1)
f(2) = (2 +1)
2 + 1.....
We now have real values from the expression.
(X² + 2X - 3) /
(x +1 ) = 3
Since it's a division process, we couldn't use BODMAS rule before applying the Multiplication and addition rules. Why? Because the expressions aren't alike. They contain unlike terms that can't be joints. So the principle of BODMAS wasn't used here.
| 5/3 .....This is the fraction we got from the division of the two expressions, making it rational. |  |
|---|
5/3........Ans ✅
Or 1.666 ~ 1.67 2 d.p
Solve the following equation: 2x + 5 = 3(x - 2) + 1 |
|---|
This equation is different from the expressions we solved because it has an equality sign that represents it. It must not necessarily be equal to zero or a constant before it's called an equation.
To solve this, we need to follow the following steps.
Step 1: 2x + 5 = 3(x - 2) + 1
We'll strike a balance on the RHS to make it appear linear as the LHS. So our focus is on the RHS.
2x + 5 = 3(x - 2) + 1
RHS.......3(x - 2) + 1
We'll open the bracket by multiplying the number outside with what's inside the bracket.
3 × X - 3 × 2 + 1
3x - 6 + 1
3x - 5......RHS
Step 2:
Combining both sides, we collect like terms, taking all the X to the left hand side and all the numbers to the right hand side.
2x + 5 = 3x - 5
C L T.......
2x - 3x = - 5 - 5
**_The explanations would be made in this video.......on how to collect like terms.
2x - 3x = - 5 - 5
- x = - 10
Step 3
Since x cannot be in negative sign as we are looking for X not - X, we'll divide both sides of the equation by -1 which is the invisible coefficient of X.
-1x/-1 = -10/-1
X = 10✅
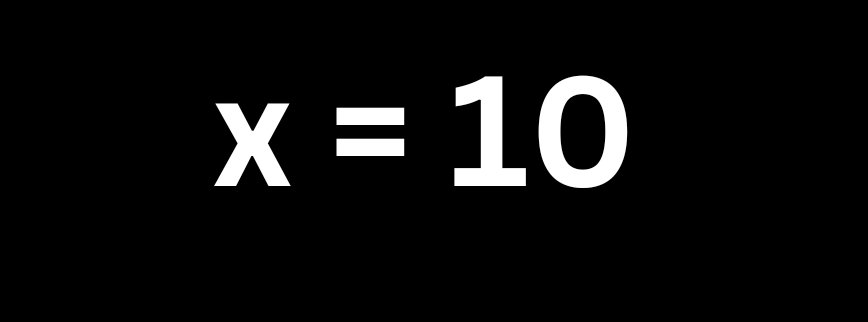
| Therefore, 2x + 5 = 3(x - 2) + 1 is 10 as X......... |  |
|---|
Task 4 |
|---|
(a.) Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit.
To solve this mathematical problem, we'll identify the parameters involved first for ease. From the question, we've seen total loaves of 250 bread per day......
- 250 loaves of bread daily.......
Let the number of white bread loaves sold per day be x.
Since the number of whole wheat loaves sold is 30 from the statement, more than the number of white bread loaves, we represent it as x + 30.
The total number of loaves sold per day is 250. So, putting everything together, we have a standard equation as;
X + (X + 30) = 250 How do we find x which is a determinant to know the number of white bread loaves. We are meant to write an expression for this. So I'll be straightforward. Let's solve for X to get the value for x.
X + ( X + 30) = 250
Opening Brackets.....
X + X + 30 = 250
2X + 30= 250
Collecting Like Terms, we keep X on the left and take the integers to the right.
2X = 250 - 30
2X = 220
To get the value of X from this equation, we have to divide both sides by 2 which is the coefficient of X.
2X/2 = 220/2
X = 110.
So we have found the number of white bread loaves sold as = 110.
Remember, the number of whole wheat bread is sold at X + 30.
Substituting X which we said at the onset to represent the number of white bread loaves into the expression X + 30, we have;
X = 110
f(x) = 110+30
140......This is the number of whole wheat loaves .
110.....This is the number of white bread loaves.
For Case 2, we are targeting daily profits of which we would still use the parameters involved to solve.
From the statement, $0.50 is what the bakery makes as profit for each white bread loaf
While $0.75 is the profit which the bakery makes from the whole wheat loaf.
To calculate total profit, we have this expression......
0.50(110) + 0.75(140)......This is the expression for getting the total profit the bakery makes daily.
Expression
Total Profit = Profit from white loaves + Profit from whole wheat loaves
Total Profit = (0.50 × x) + 0.75x × (x + 30).
where X = 110....
($0.50x) + (x +30) × $0.75x)..........✅
P = $55 + $105 = $160.
Therefore, the total daily profit of the bakery is $160
B. Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hour's then write an expression for the total cost of renting the car for x hours and show how you simplify it.
To write a clear expression for the total cost of renting the car for x hours, let's take these conditions.
Condition 1: Cost of renting a car for a day as shown in the statement is represented by;
2x + 15.......where X in the expression is the number of hours the car is rented.
Condition 2: Company offers a package cost at;
3x - 2 where x > 4
Therefore, the total cost for renting the car for x hours is expressed as;
Total Cost = (2x + 15 ) x ≤ 4
(3x -2) x > 4
If x ≤ 4: Total Cost = 2x + 15. and,
If x > 4: Total Cost = 3x - 2.
To simplify each conditions, we'll take note of some criterias.
Condition 1: If x ≤ 4 =
Total Cost remains 2x + 15 because the expression is simplified already and won't need further simplification
Condition 2: If x > 4, then the total Cost remains 3x - 2 because the expression 3x - 2 is also already simplified as well and doesn't need further simplification.
The expressions are stated below.
- Trent the car for 4 hours or less which is ≤, the total cost for doing so is 2x + 15.
- To rent the car for more than 4 hours which is >4, the total cost is 3x - 2.
The expression cannot be further simplified because the cost actually depends on whether the value for x is less than or equal to 4 or actually greater than 4.
I invite @artist1111, @whizzbro4eva and @toflex
All images are gotten from my phone and Canva Application
Cc,
@khursheedanwar
Comments