SLC21 Week4 - Recursia

_{Design On Canva}

Recursion is a technique in programming in which a function divides a problem into smaller instances and then calls itself to solve them, eventually leading to a fundamental direct solution. Each call that comes solves one part of the whole problem, thus solving them, they reach the main conclusion where the final decision is made. As we have seen this repetition before, in factorials, in Fibonacci sequences, and them, we have seen recursion of such things.

Shapes that exhibit self-similarity at different scales, which are metric shapes, are fractals. They are geometric shapes that are related to recursion. Fraction is also like recursion, in that a part is a smaller version of the whole. Like recursion, we break them down into smaller problems and solve them. In both cases, the idea is central to repeating itself, on different scales.

To find the limit of the largest factorial we can have with a given data type, we need to examine the maximum values of each type. Because factorial values grow very quickly.

Below I present a table indicating the approximate maximum values of the factorials in C / C++.

Explanation:

chart: It can hold values of 127 for signed and 255 for unsigned because the highest factorial is 5! = 120

short: It can hold 32767 values for signed because its largest factorial is 7!=5040.

int: It can store 2,147,483,647 values because its range is 12! factorial= 479001600.

long and long long: They can hold up to 9223372036854775807 values and allow 20!

float: It can handle approximately 34! floating point values before reaching the limit.

double: This allows us to have large values before our problems which is around 170!

long double: This gives the best prediction up to a factorial of approximately 1754!

These are all limits and may vary depending on your system and compiler. You can calculate your factors using an iterative method to find a good and large factorial.

To know how many times recursive calls are made in a function, we first have to understand the concept of stack overflow because every time a function calls itself, a new frame is added to the stack. That saves the state of the function and similarly when the stack is full, then overflow occurs and as a result, the program terminates.

There are some steps to find out how many times our system makes recursive calls to terminate the program. The steps are given:

Endless Recursion:

First, a function will be created that keeps calling itself and does not stop. This function will keep calling itself until the stack space runs out and at the end it will show us an output telling us how many times this function was called before the program crashed.

Here is the C++ Code:

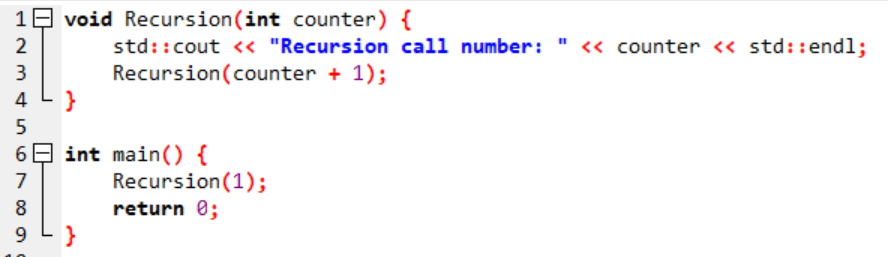
Recursive Factorial Function:

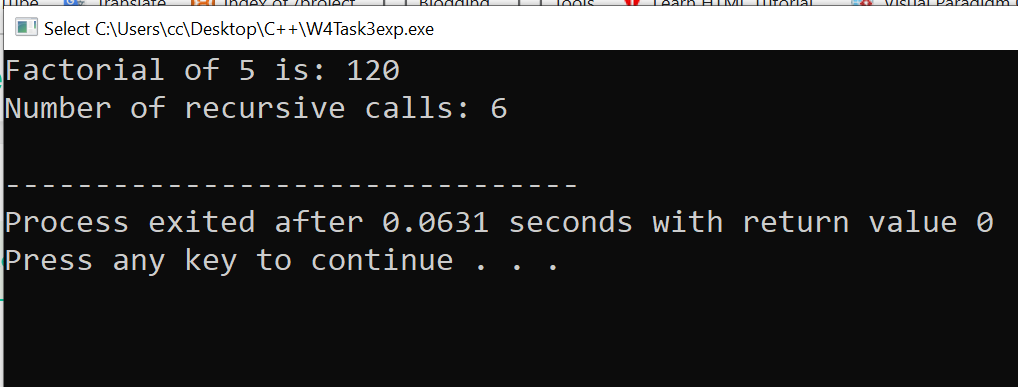
To prevent the condition, we will take a clear example, which is calculating the factorial. Note that the counter will keep track of how many calls have been made. Because for n=5, there will be six recursive calls.

Here is the C++ Code:

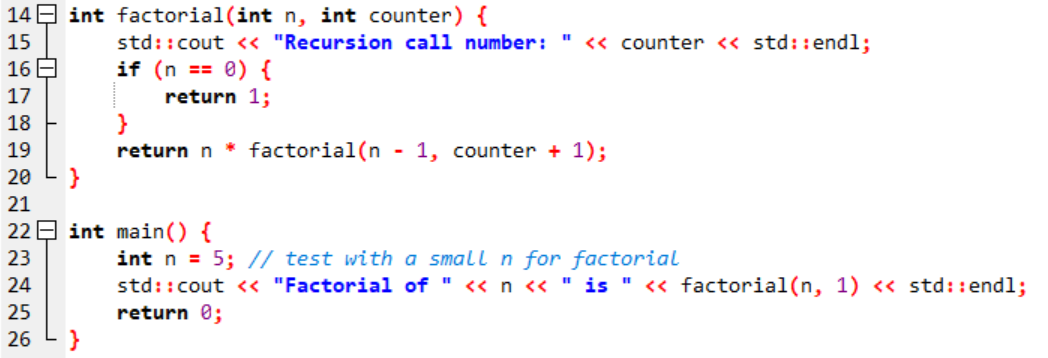
Measuring Maximum Recursive Calls:

Here we can modify our recursion function to see how many times the recursion happened before crashed. This will tell us the exact values by measuring.

Here is the C++ Code:

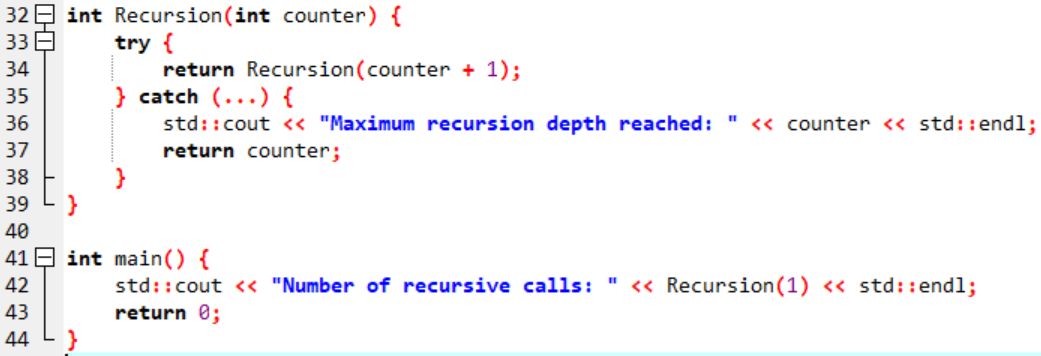
Full Example of Recursive Factorial Function with Call Counting:

Here is the C++ Code:

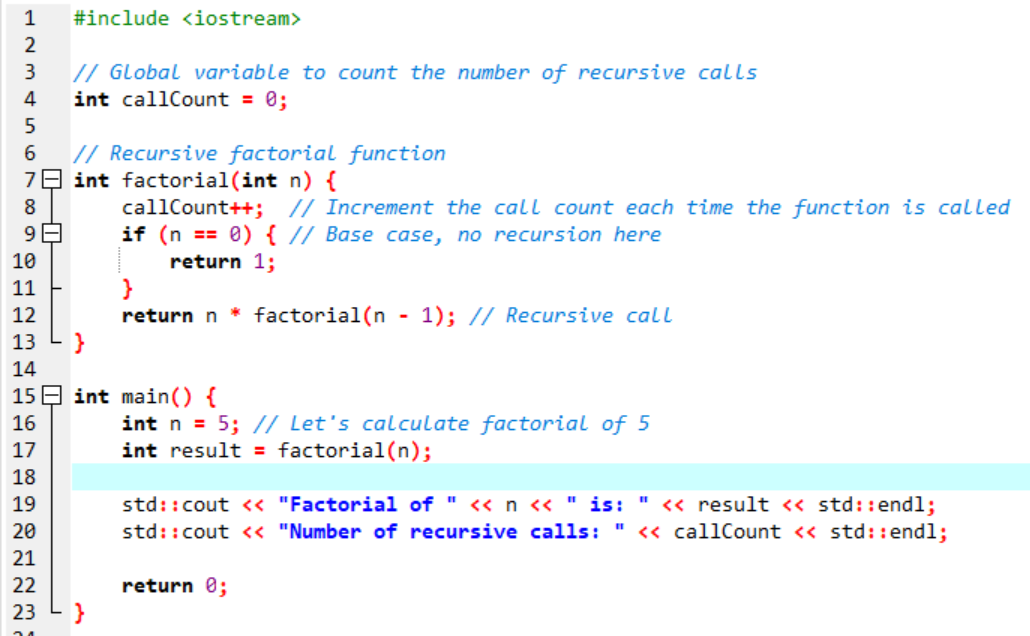
Here is the Output:

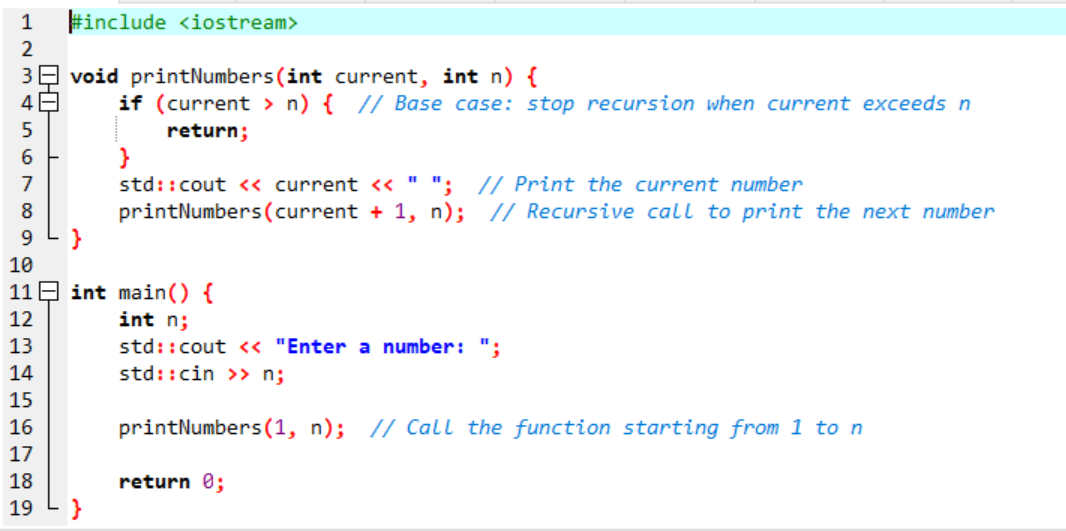
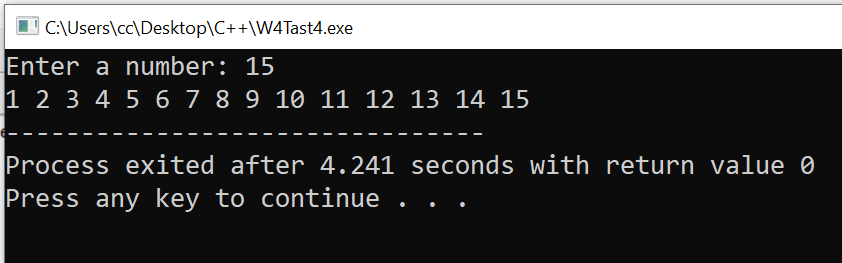
Using recursion we will print the numbers from one to n. For this, we will first create a recursive function that will print the current number and then it will call itself and take it to that number until n is reached.

Here is the C++ Code:

Here is the Output:

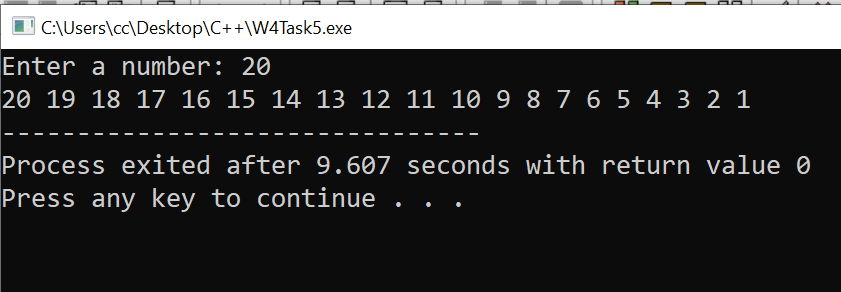
To print the number from n to one using the recursive method, we only need to modify n in the recursive function and then decrement the number until it reaches one.

Here is the C++ Code:

Here is the Output:

Using Loop

First, we will use a loop to add two numbers. We will use a loop to increment one number while decrementing the other until the second number is zero.

Here is the C++ Code:

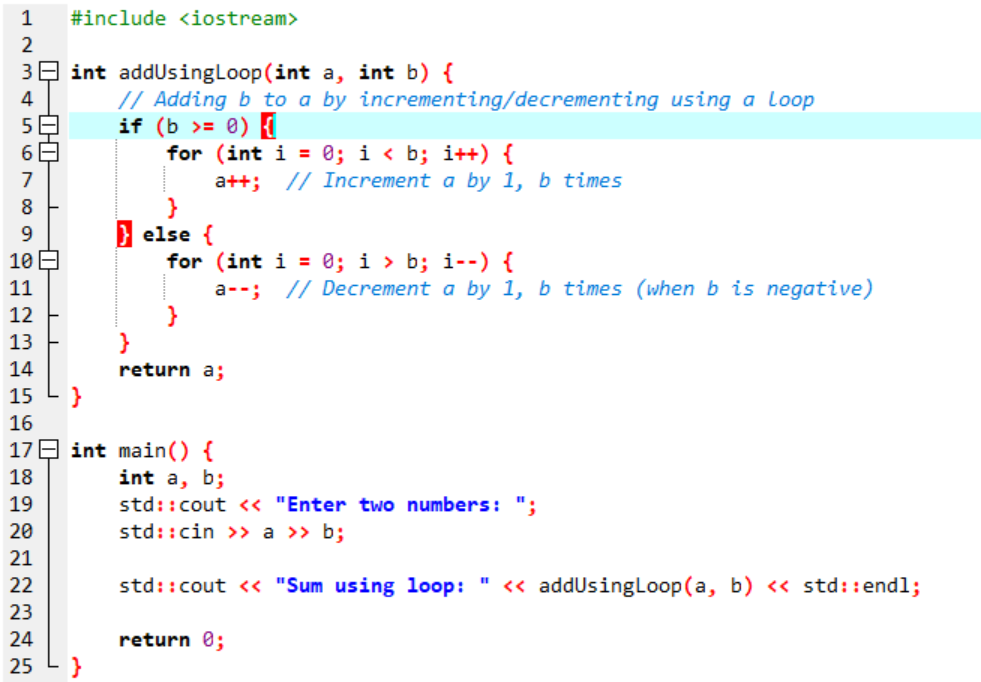
Here is the Output:

Using Recursion

We will perform the same function with the recursion method in which if we have B positive then we will increase A and decrease B until it becomes zero and similarly if we have B negative then we will decrease A and increase B until it becomes zero.

Here is the C++ Code:

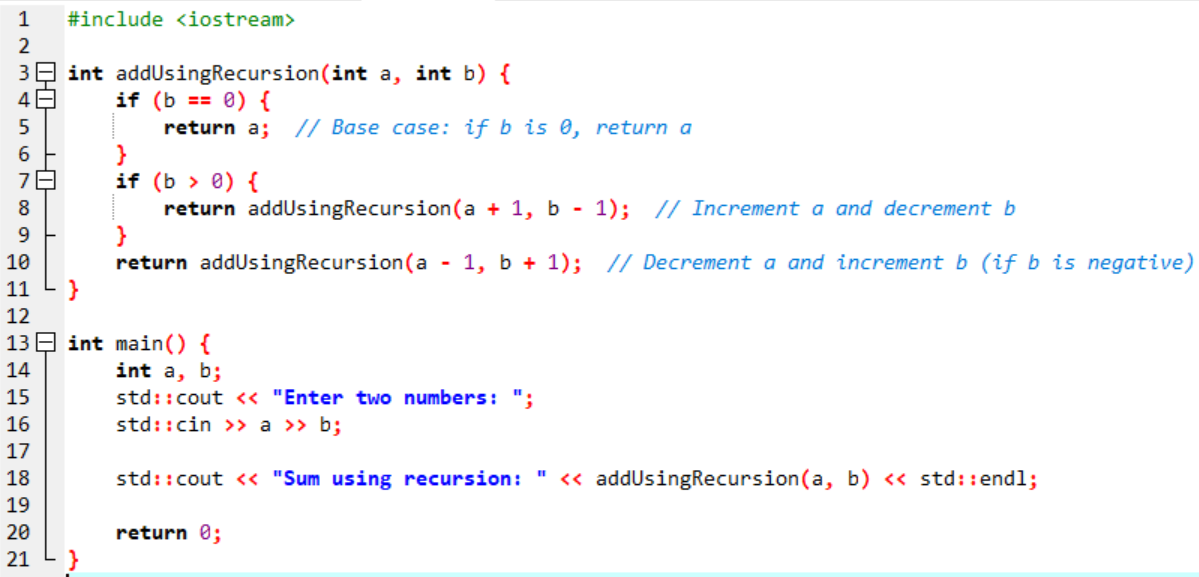
Here is the Output:

Using Loop

In C++, we can print a string character by character by treating the string as an array of characters.

Here is the C++ Code:

Here is the Output:

Using Pointer Dereferencing

We can also use pointed dereferencing to print a string. This highlights the use of pointers to access each character in the string.

Here is the C++ Code:

Here is the Output:

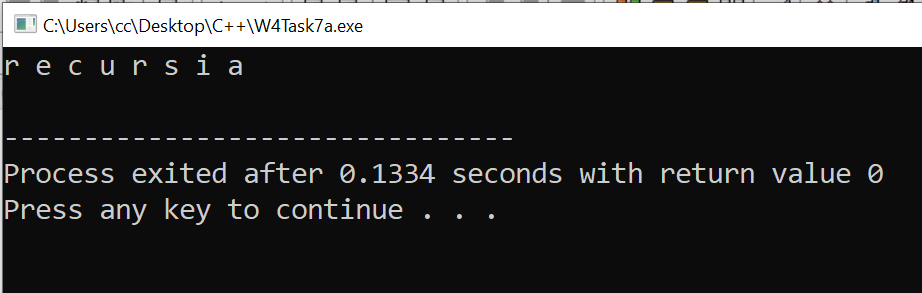
Using Loop

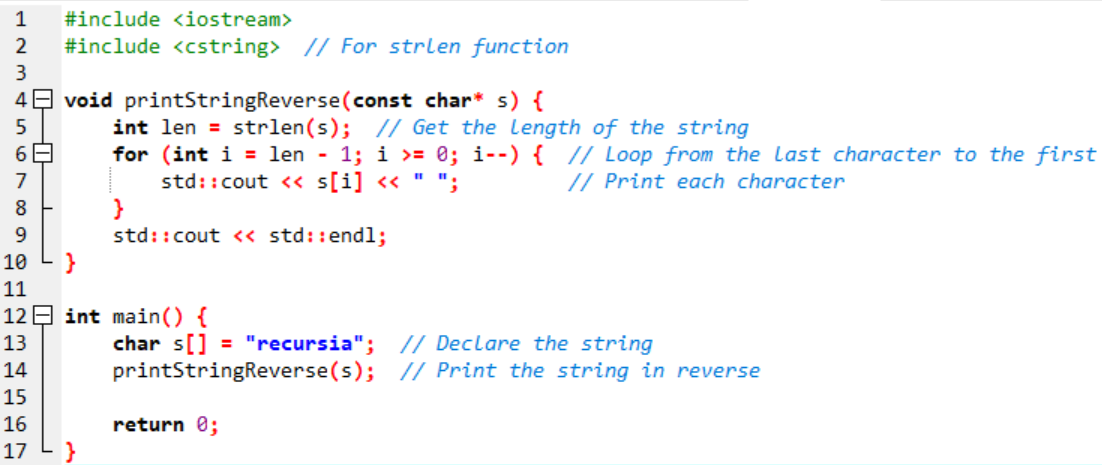
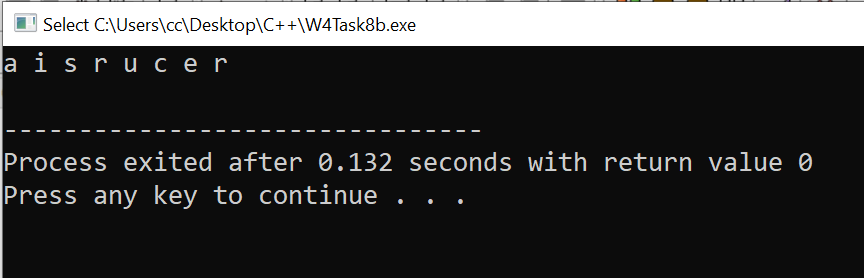
We can print the string in reverse, starting from the last character of the string. This will first find the length of the string and then print the characters starting from the last character.

Here is the C++ Code:

Here is the Output:

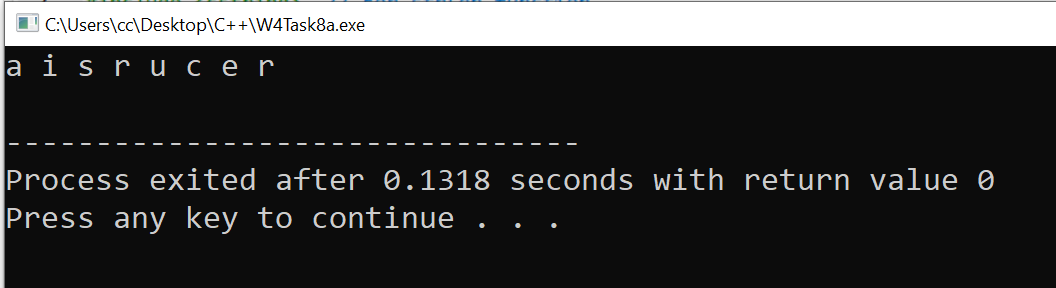
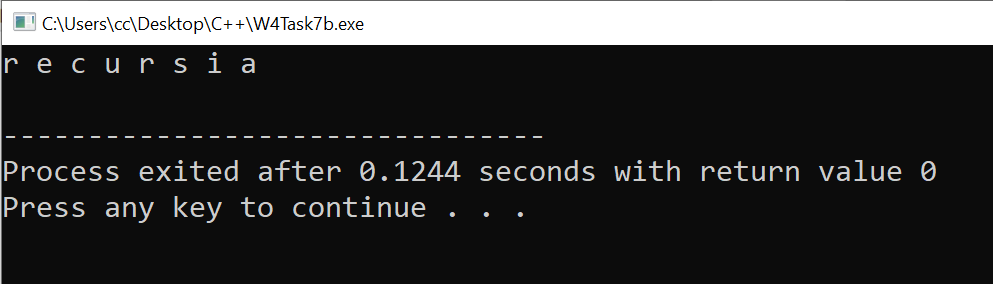
Using Pointer Dereferencing

We can also reverse a string using pointer dereferencing by going to the end of the string and then working backward.

Here is the C++ Code:

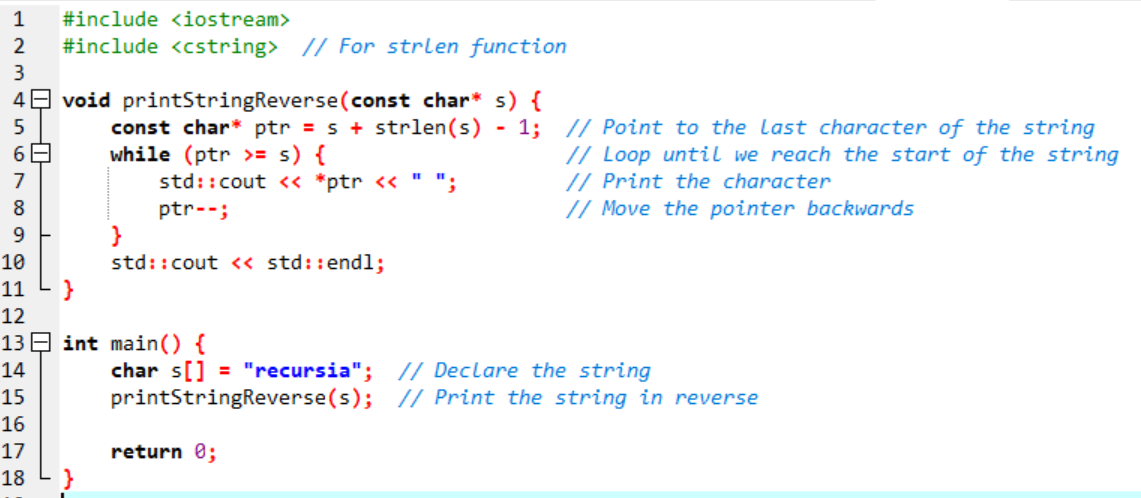
Here is the Output:

Thank you so much for staying here. I hope you guys like my task work. I would like to invite @kouba01, @josepha, @abdullahw2, and @rumaisha to join this task.

Cc:
@sergeyk

_{Dated: 20-11-2024 About Me}