SLC21 Week2 - Programming arrays
4 comments
This is the Homework with the corresponding tasks for the SLC21 Week2 - Programming arrays by @sergeyk!

Image taken from Pixabay
Brace yourselves, this is going to be a long post!
Let's get started!

Declaration of arrays, created a few examples in the screenshot below:
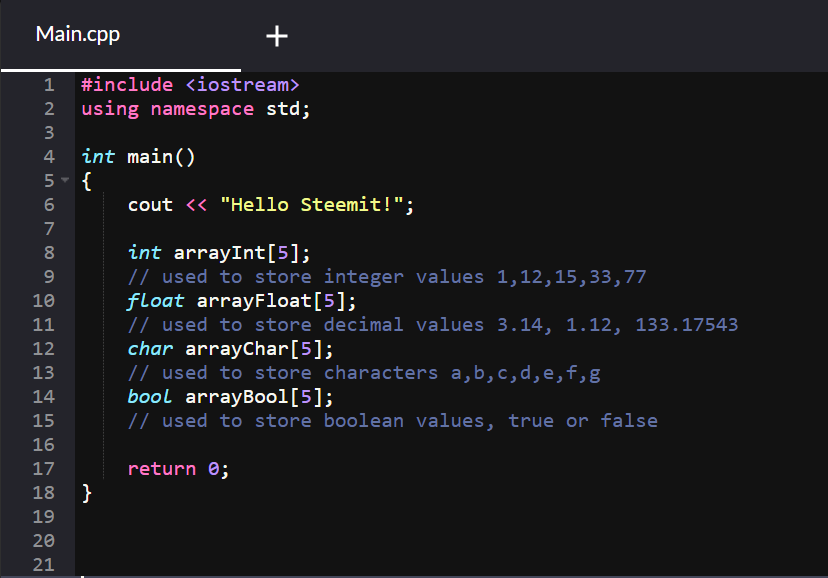
We are going to use the arrayInt one for further explanations. We declare it like this int arrayInt[5]; where 5 is the size of the array, meaning we can store 5 integer values in arrayInt.
Let's see how can we store values in this array, there are multiple ways, let's go through some of them with examples.
We can do it directly while declaring the array, we store the values inside brackets { }.
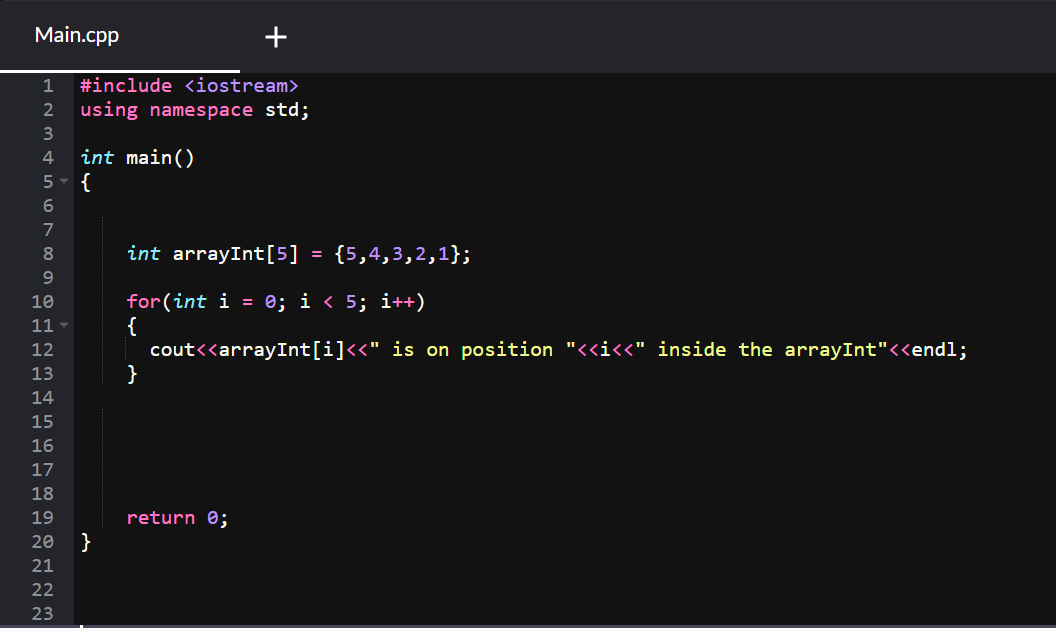
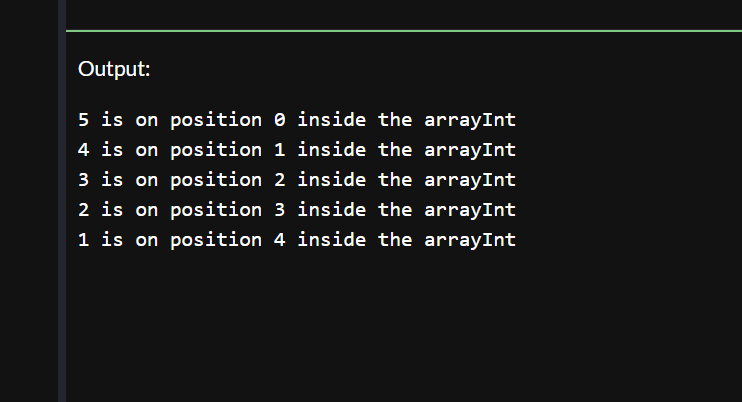
We are using a for loop to go through the values and print them to see if our array is working properly. The output when we run the code above is as it follows:
Now in this case if we are having 5 slots for our numbers but we fill only 3 of them the rest will be automatically filled with 0 or a random number in the int range, so you need to be careful while doing it and make sure this won't break your code later on.
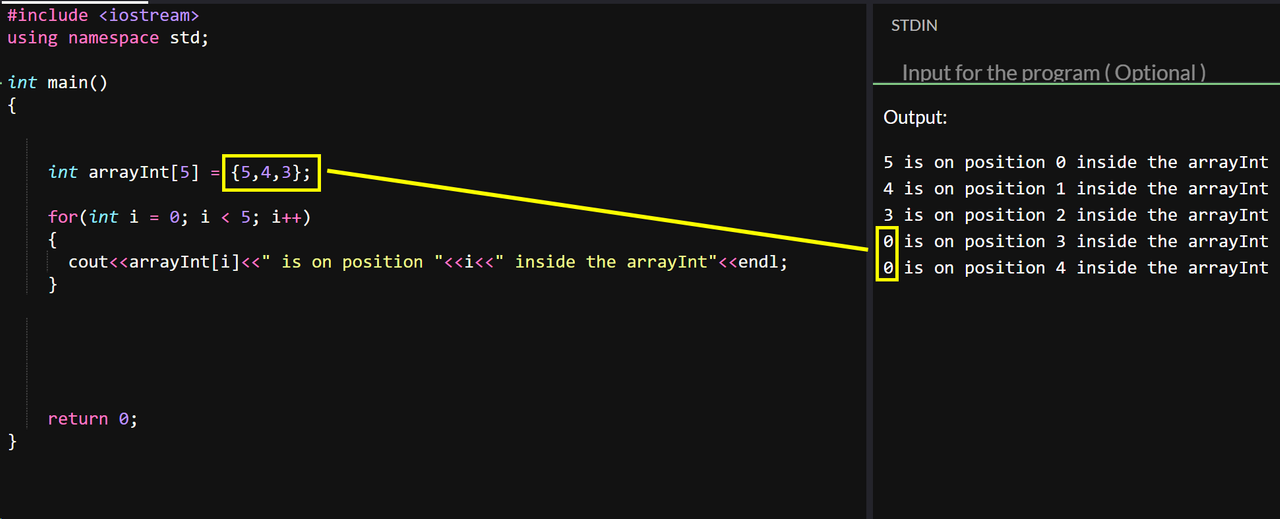
As you can see I only assigned 3 values to my array so the other 2 slots were filled with 0s this time.
Let's see how else can we use our array and assign values to it. We can do it individually for each position of the array, like this:
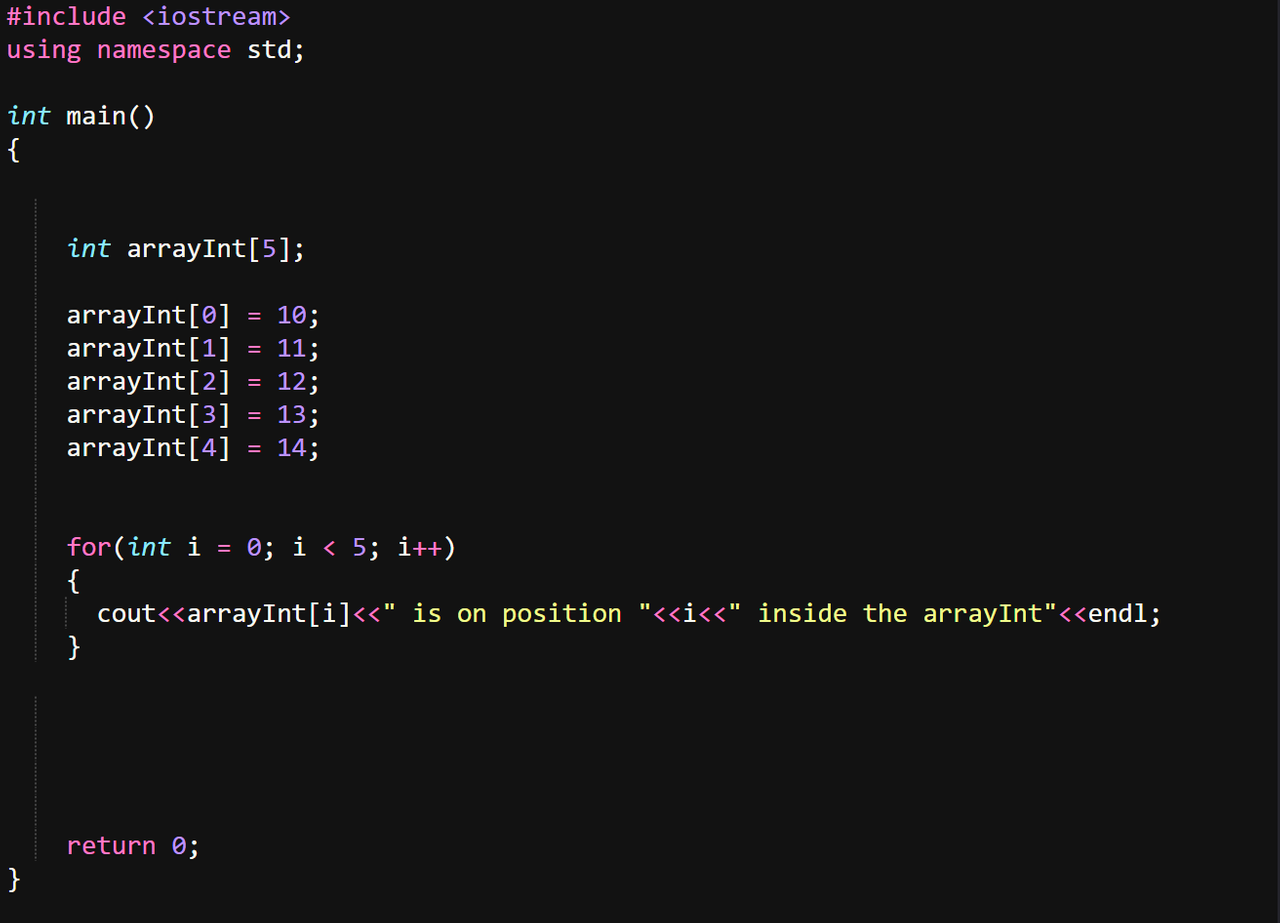
The output for this method looks like this:
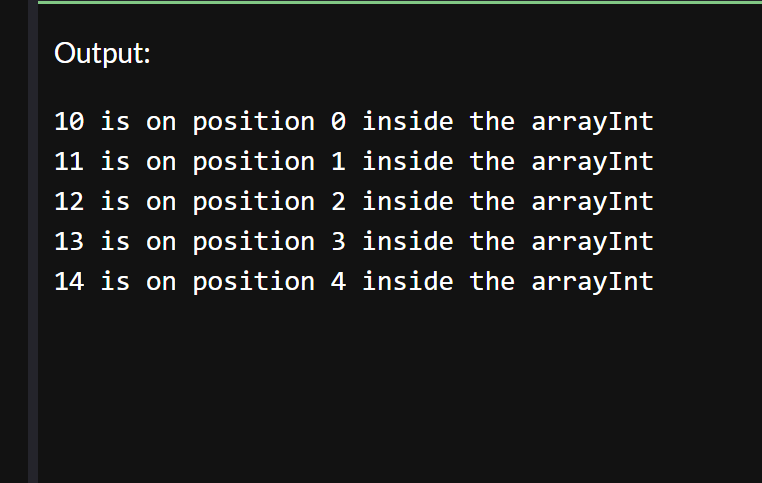
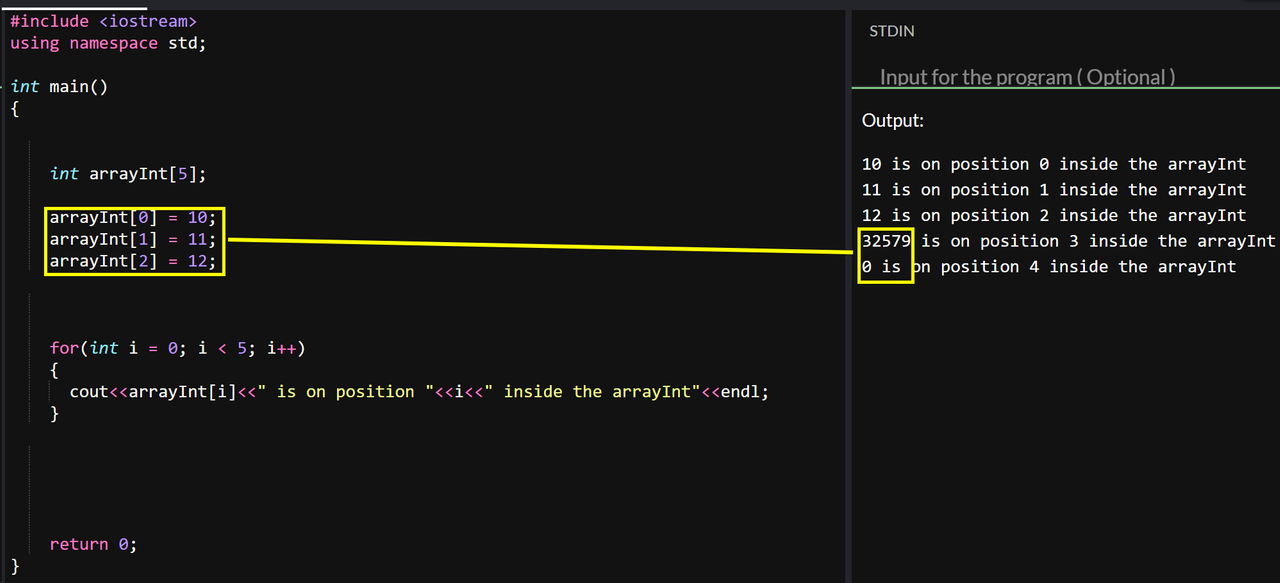
In this case we need to be careful as well as in the previous one, you miss one or multiple positions and these will be filled with 0s or a random number in the int range. In the following output you can see one was set to 0 and the other a random number in the int range.
Another method is to get the value as an input from the user using cin>>variable, it should look as it follows:
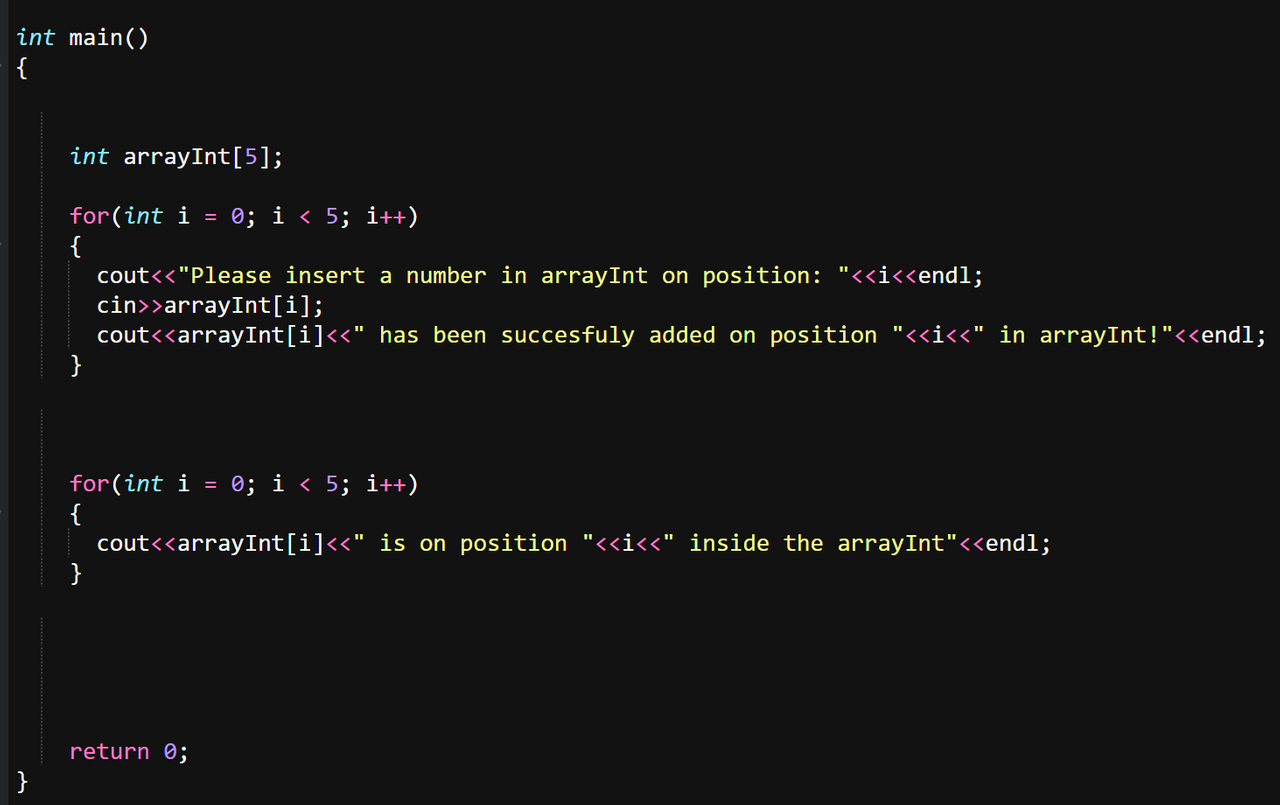
With the Output looking like this, as you can see in this case we are going through all 5 positions and making sure each one gets the desired value.
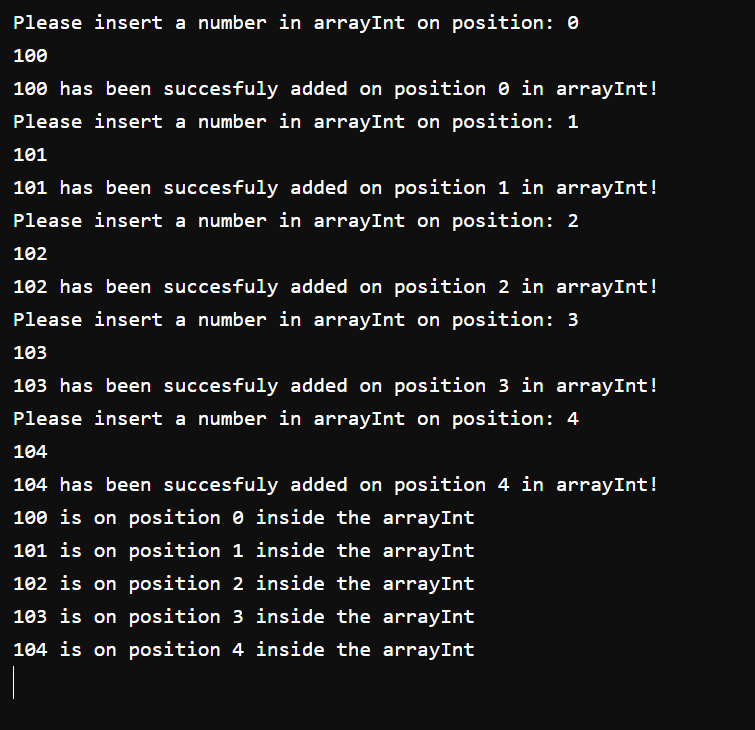
Giving a too big of a value that gets outside the int's range will return errors/timeouts!
Now let's see how can we access the values inside an array, we can do that using it's position to get to the actual value.
The advantage of arrays over normal variables comes in the storing management where you can store multiple values in a single variable and use an index to go over them, reduced complexity because you have 1 variable vs multiple ones, and it is also memory efficient and reduces program size.

The name of an array is used as an identifier, it helps the user make difference between multiple ones and gives it uniqueness.
If we try to print the value of a without it's position it will result in the address of a, since it's only a without any addition it's a pointer to the first element of the array. Let's see an example:
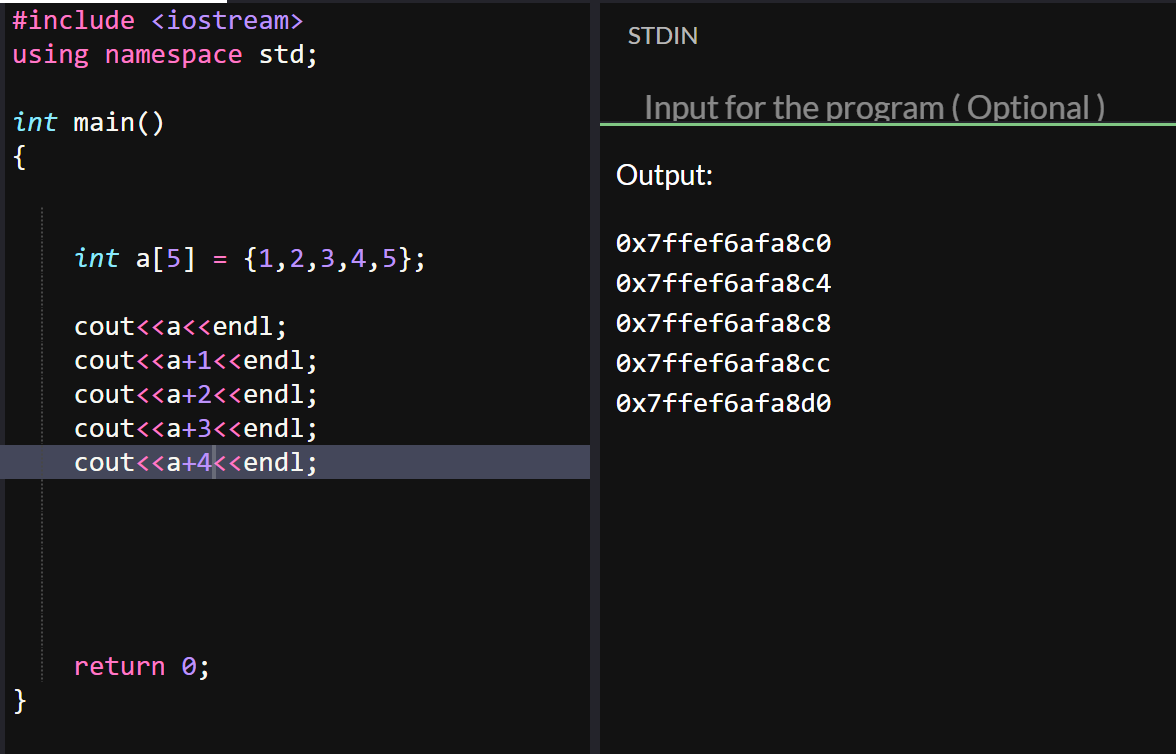
Each row represents an address for one of our elements, in the output order it starts with the first position and goes until the last one.
If from this point we want a way to access the actual value we could use a pointer (noted like this *) that will point to the address location and retrieve the actual value stored in that address.
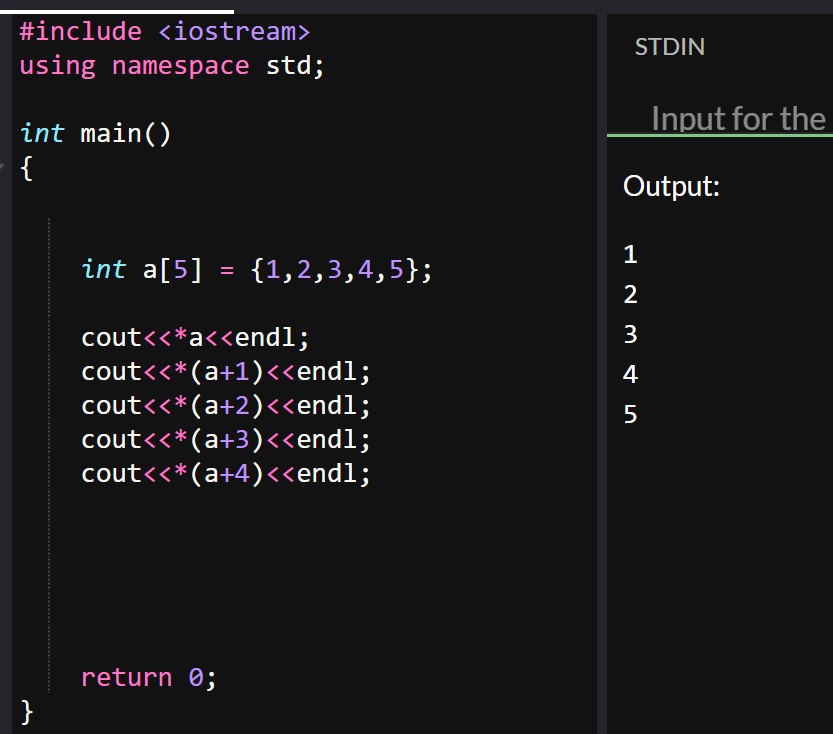
Now let's check the cout<<a+2 and cout<<a-2:
cout<<a+2 as described in the images above will return the address of the second element in the a array.
cout<<a-2 on the other hand will return the address that is two elements before the start of our array a.
Now if cout<<a outputs the address 4000 cout<<a+1 can return as it follows:
If a is one of the following:
int, it has the size of 4 bytes and it will return 4004.
float, it also has a size of 4 bytes and it will return 4004.
double, this one has a size of 8 bytes so our return will be 4008.
bool, with a size of 1 byte will return 4001.
char, has also a size of 1 byte and with this returns 4001.
And there are other data types each one with it's size, a table could look like this:
| Data Type | Size (bytes) | a (4000) | a + 1 (next address) |
|---|---|---|---|
int | 4 | 4000 | 4004 |
char | 1 | 4000 | 4001 |
float | 4 | 4000 | 4004 |
double | 8 | 4000 | 4008 |
bool | 1 | 4000 | 4001 |
long | 4 | 4000 | 4004 |
long long | 8 | 4000 | 4008 |

Yes there are double sized arrays, they are called matrix and to describe it as easy as possible imagine a table with rows and columns where each row is an array with the same size, the size of each row can't be different.
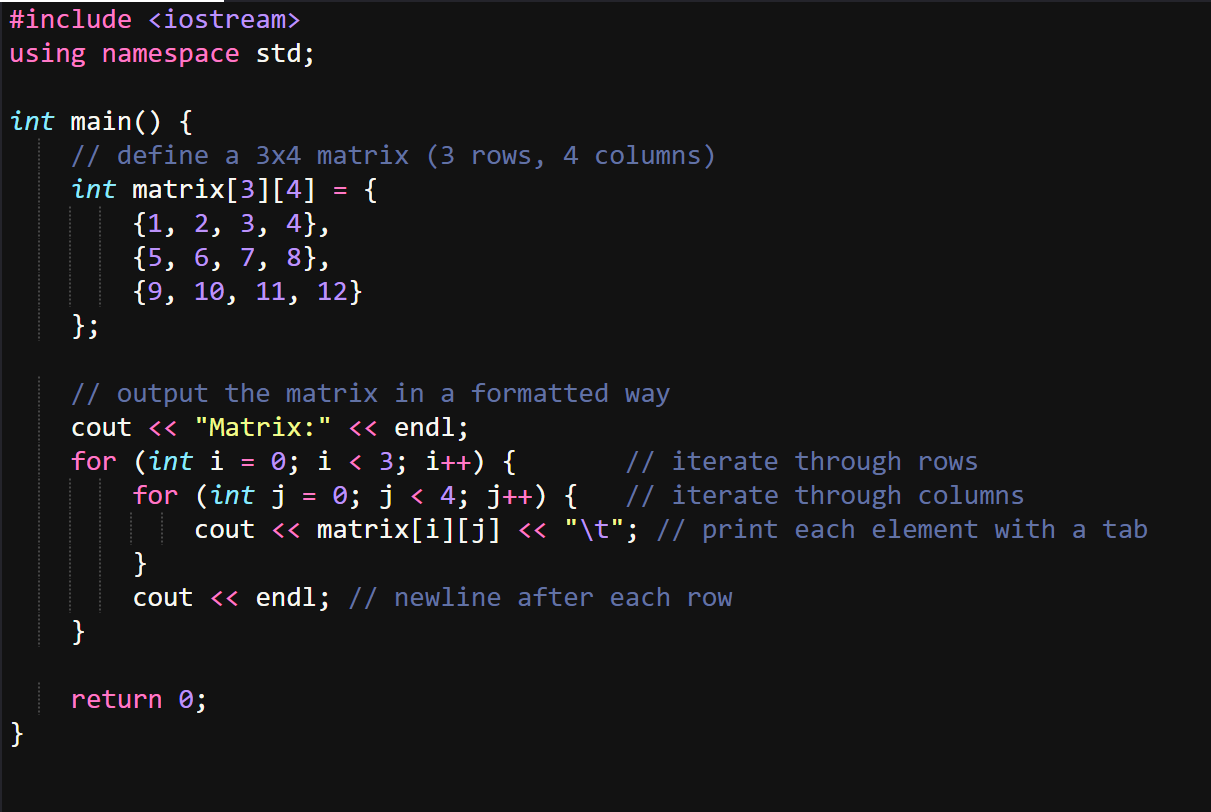
The matrix has X number of columns and Y number of rows. You can declare it as it follows in c++. int myMatrix[5][7];, in this case you need two indices to access the value one index used for the columns and one for the rows and these two pinpoint to the exact slot in the matrix to retrieve the value.
I created a simple visual representation so you can get an idea, it looks like this:
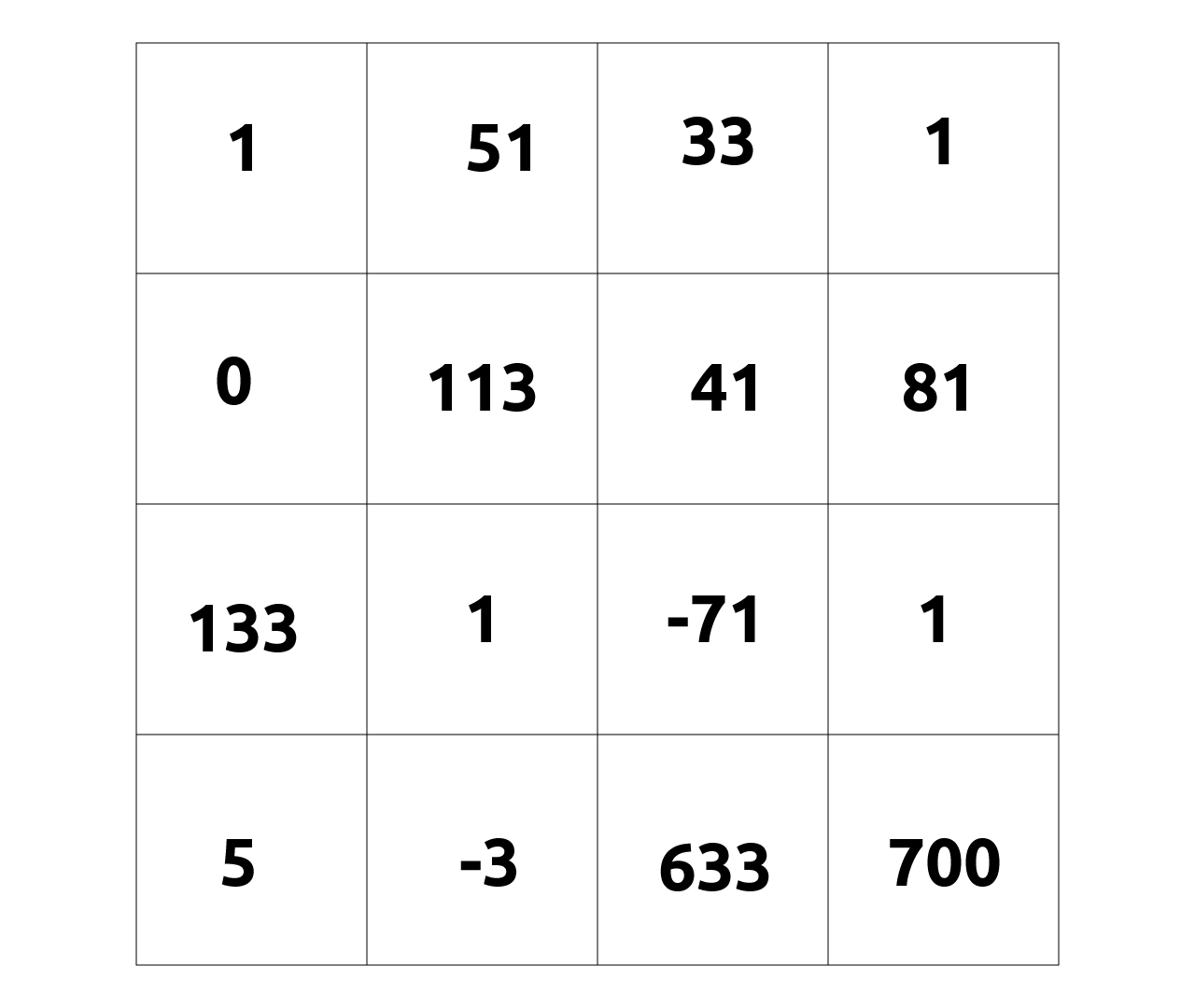
This is a 4x4 size Matrix using integer values. And let's see a code example:
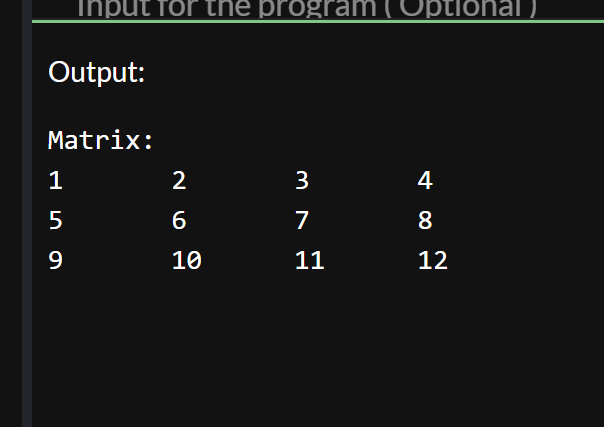
And it would have this output:

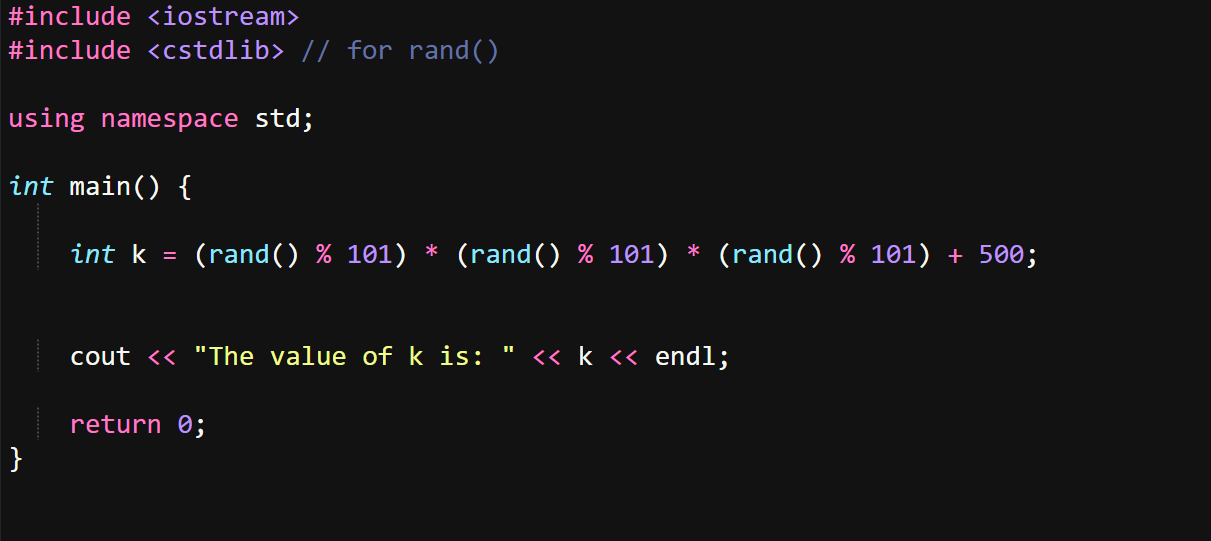
int k=(rand()%101) * (rand()%101) * (rand()%101)+500;
Let's first write the code for our K variable. We need to make sure to include cstdlib to make the rand() available in our code.
The code would look like this, and once ran we get a random K which is not really random after each try in this case, we get the same value each run because in C++ if you want to use rand() and get a new value each time you need to seed the time() function from ctime lib to the rand() function, getting a new seed each time means a new value for the rand(). But for the sake of our task we are going to keep it simple, we are looking for the divisors of a number here.
Now for the divisors, there are multiple ways to do this, using normal function, using a recursive, grouping divisors, each one with it's pluses and minuses. For this one we are going to simply use Divisors pairing, something simple to understand and still efficient. This is one of the first things you learn in highschool at computer science while working with divisors if I remember correctly.
Let me explain the concept below:
What are these divisors you might first ask yourself?
The divisors of a number are the numbers to which our main number divide perfectly:
Example for number 8:
1,2,4,8 are all divisors of 8 because if you divide 8 to each one you get a rest of 0.
5 for example is not a divisor because 5 goes one time into 8 and we get a rest of 3.
Now for this Divisors method the concept is that divisors always come in pairs. For each divisor of our number k there is a corresponding paired divisor with the form k/divisor. In this case if we move through all divisors from 1 to square root of k ```sqrt(k), we should only loop until we reach the specified square root.
Let's code this, it should look something like this (also added some comments on the code):
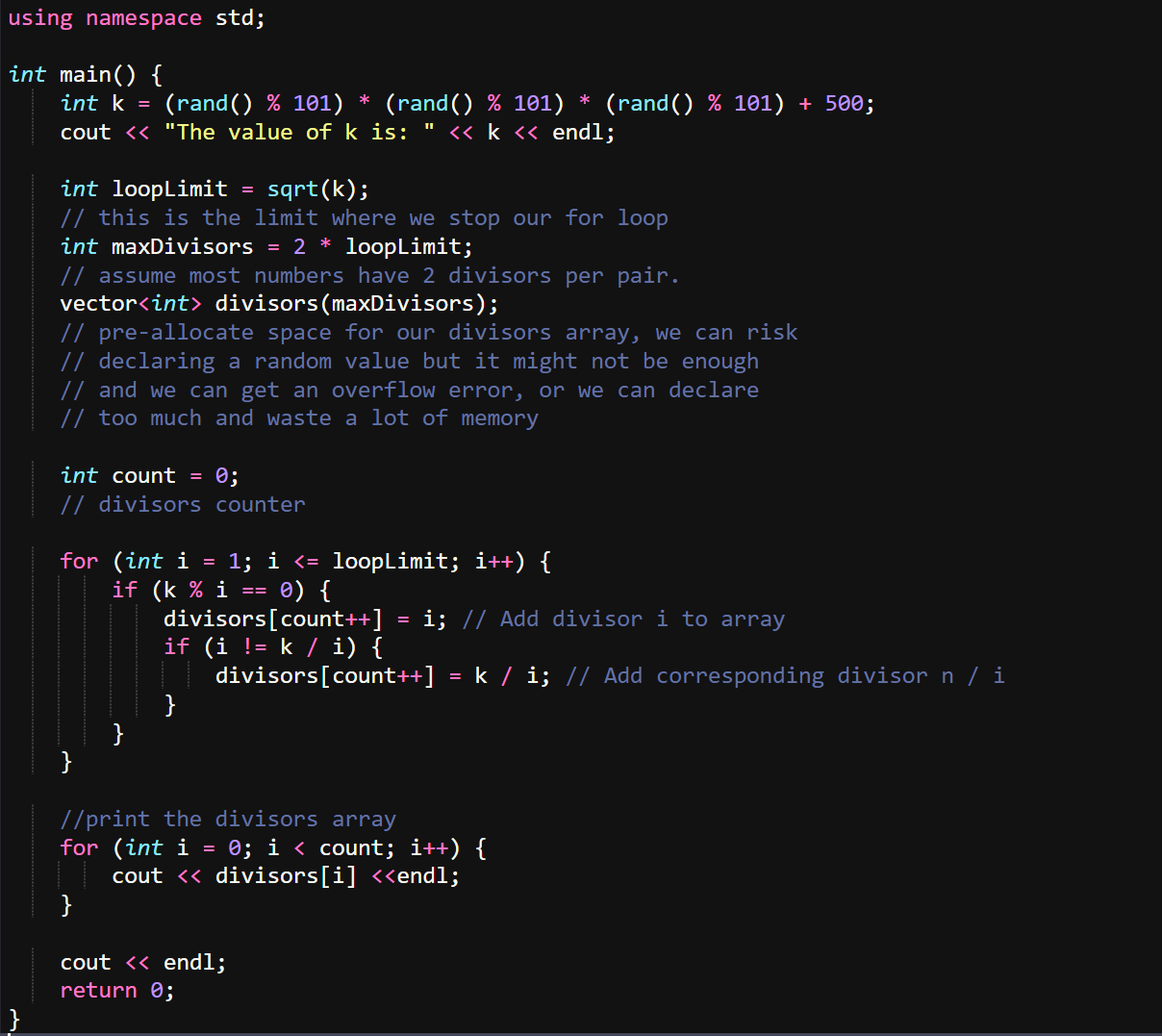
And this is our output, it looks like this in pairs [one small value, one big value] because here is the efficiency, we work on both ends of our number.
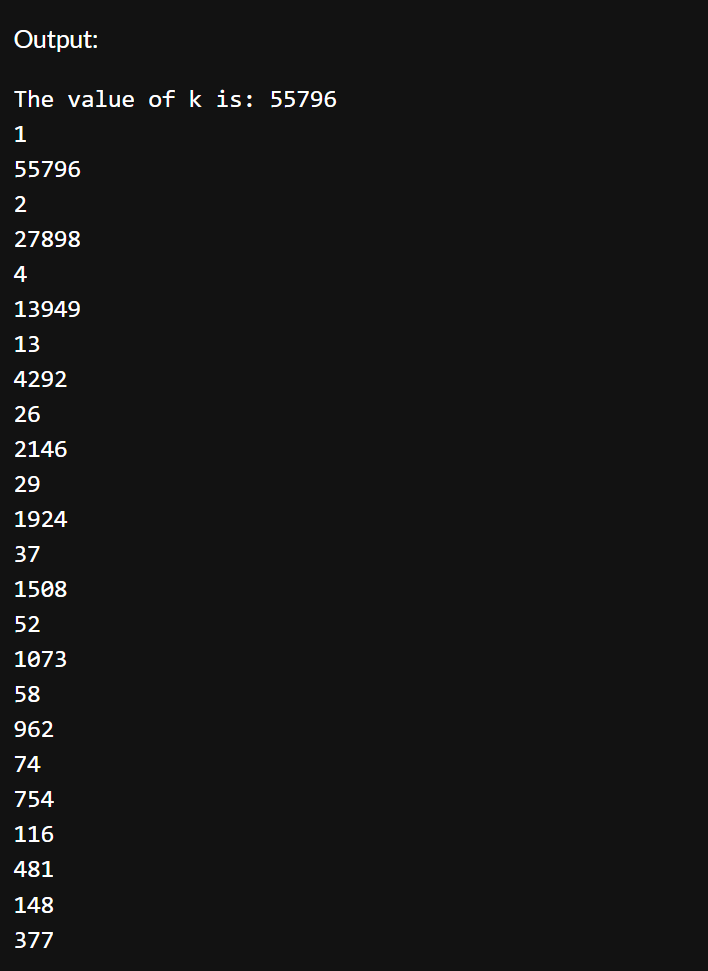
In this case our K had a big value, let's try a couple of runs with some smaller numbers where we can call the divisors from the top of our heads and make sure it's working properly.
K = 8 returns:
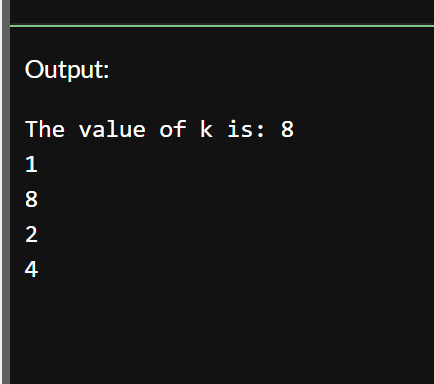
K = 32 returns:
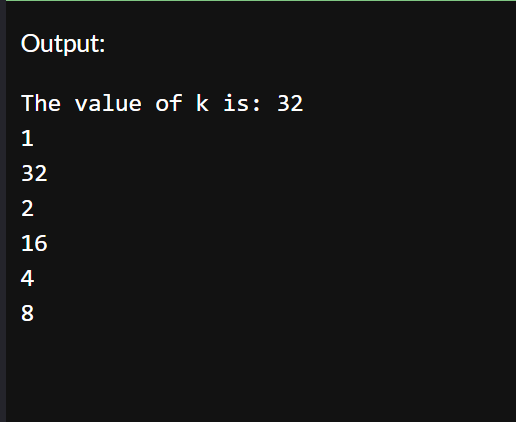
K = 21 returns:
To end this concept of Divisors pairing with a live example, it would be like this:
Let's assume k = 36, and we loop through each number i in our loop, i = 1,2,3,4,5,6 ... and so on, if i is a divisor for our k, then the rule is that k/i is also a divisor.
k = 36 -> 1 * 36 = 36, 218 = 36, 312 =36 and so on...

Now as far as I understand from the google translation, we have to declare an array with a size of 55, we fill it with random numbers from 10 to 50 and after that we check the array and if we find number 37 we can break out of the loop checking and print yes, if there is no number 37 inside the array we simply print no.
Let's see how this should look like.
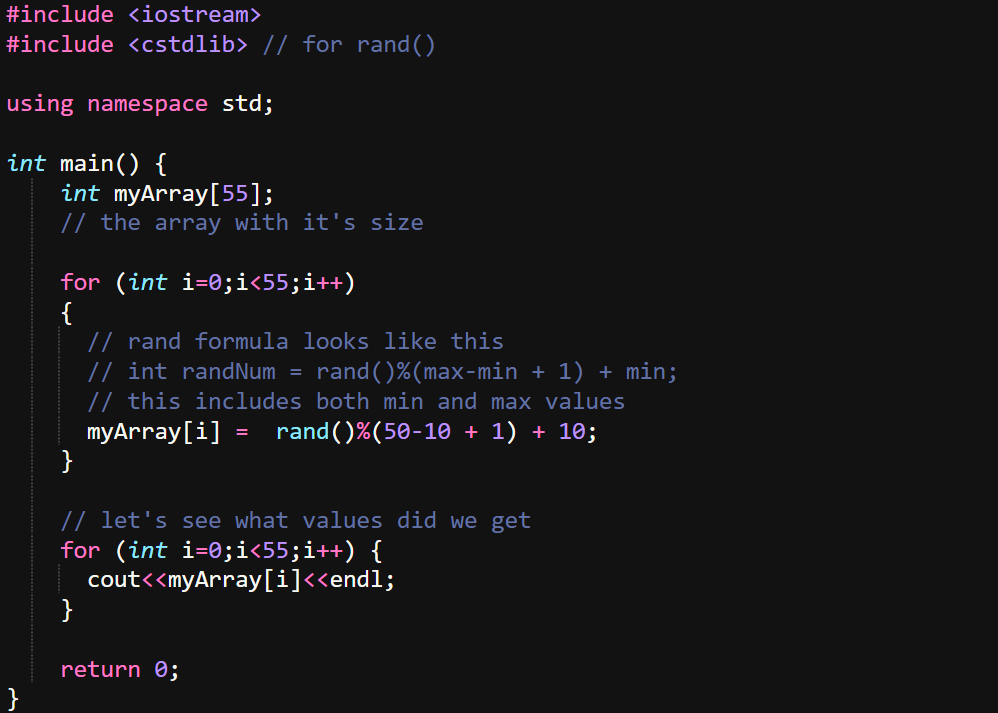
As you can see to generate a random number between two values, min and max in c++ we need to use this int randNum = rand()%(max-min + 1) + min; to make sure our number stays inside the range and includes both min and max values.
How does this keep a number in our range, let's see a small example:
The rand() returns a value of 1337, using the rand() % (max - min + 1) modulus operation we get 1337 % 41 (max - min + 1 = 50 - 10 + 1 = 41).
1337 % 41 is 32 with a rest of 25, to this we need to add our min because it doesn't start at 0, so we get 25+10 it's 35, which is in our range [10;50].
Now let's do the check and it would look like this:
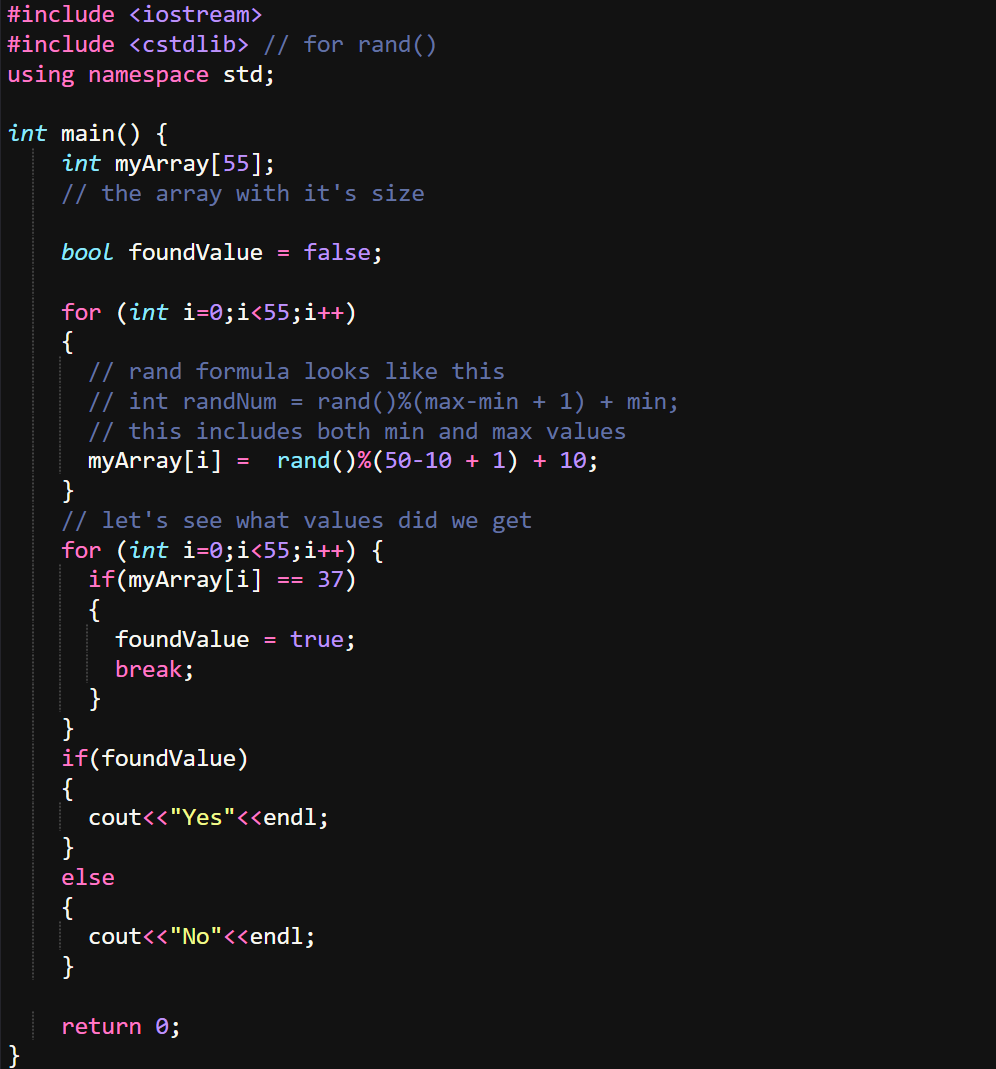
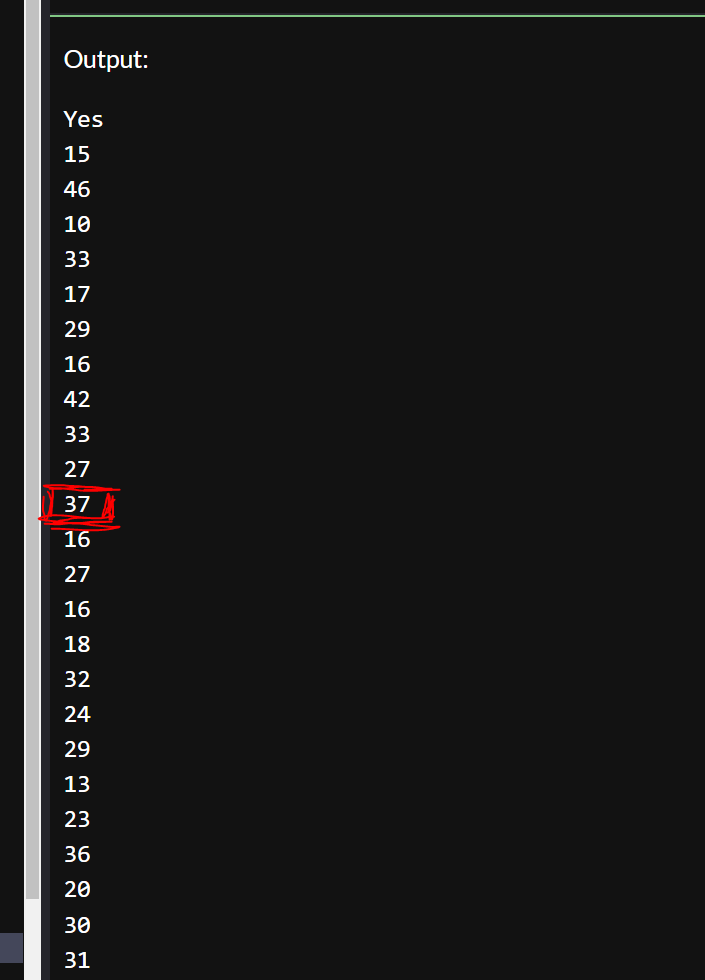
And in this case our output is Yes, we have value 37 in our array, part of the output below:

In this task we need we have an array with 66 randomly generated numbers between 12 and 60 and we need to replace even elements with 7 and odd with 77, we'll reuse the code above to generate these numbers.
This is the code that generates our array:
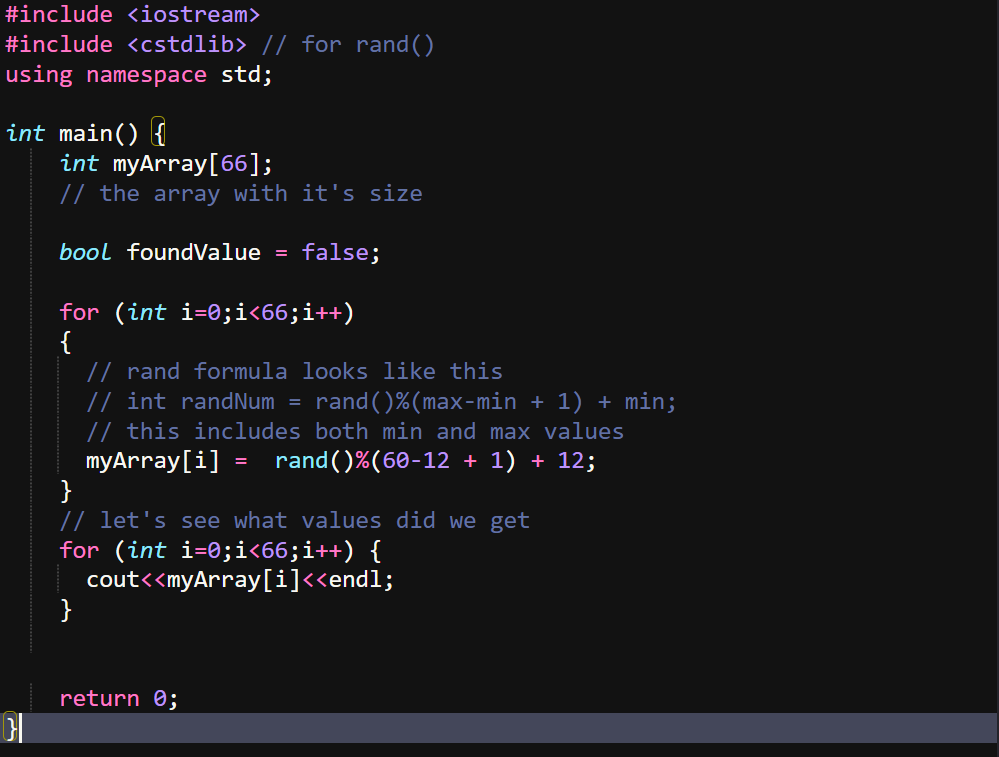
We have the array prepared now let's see how are we going to replace the odd and even numbers, we are going to loop through the array and do a check, based on the check result we replace the value as needed.
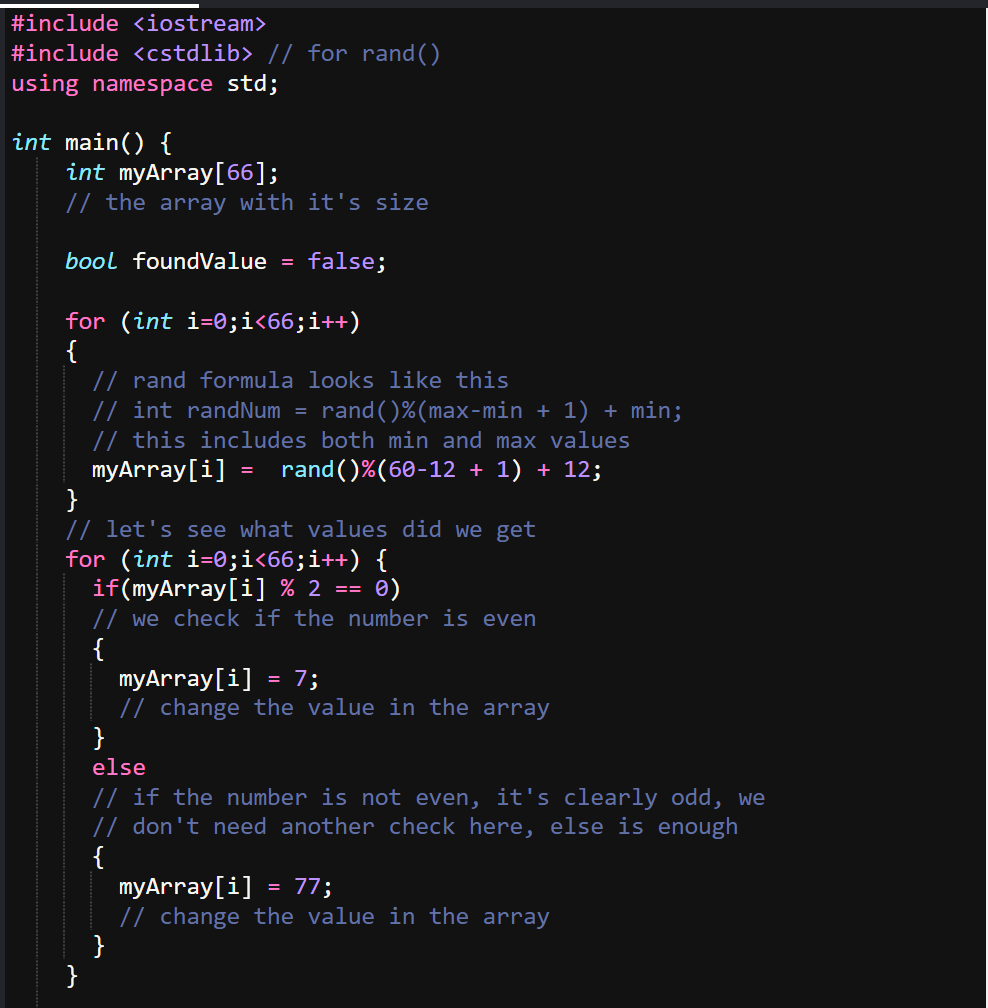
Let's compare the results below:
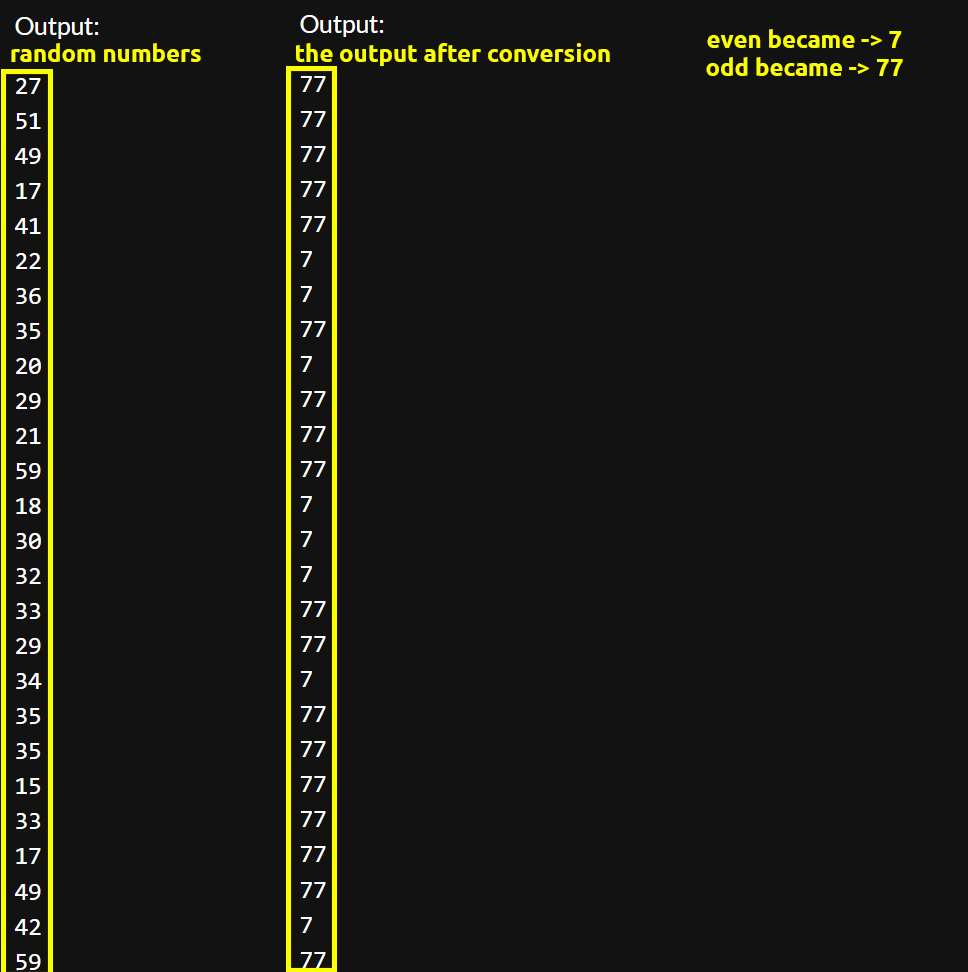
As you can see it worked, the numbers were replaced accordingly based on the modulo division we used in our condition.

In this last task we have an array with a size of 77 elements, filled with numbers from 102 to 707 and we need to find the two largest numbers.
Let's reuse the code above and generate our 77 elements between 102 and 707.
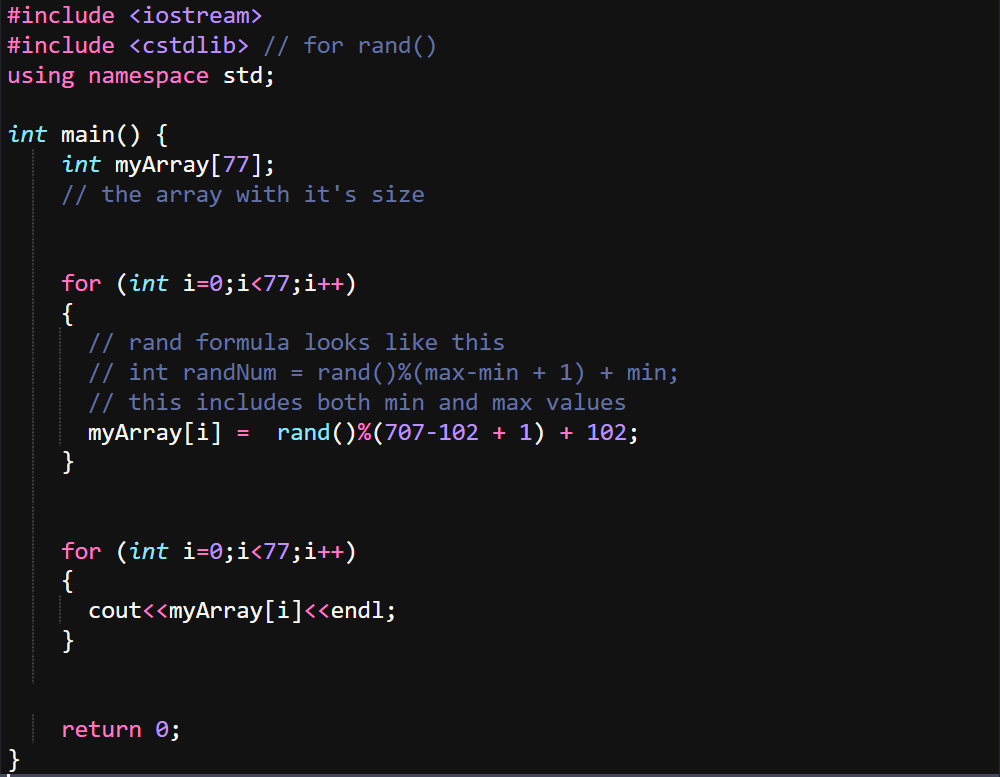
What are the two largest numbers in an array? The two largest numbers in an array are the two biggest numbers stored.
Example: 1,2,3,11,5,7,8,33,0 -> two largest numbers are 33 and 11
How can we find these two largest numbers, there are many ways to do it, we can use two variables one for the firstLargest number and one for secondLargest number and use them to compare values while looping through them, this is an efficient way because you loop through the array only one time and store the highest values in the two variables.
This would look like this, more details in the comments inside the code:
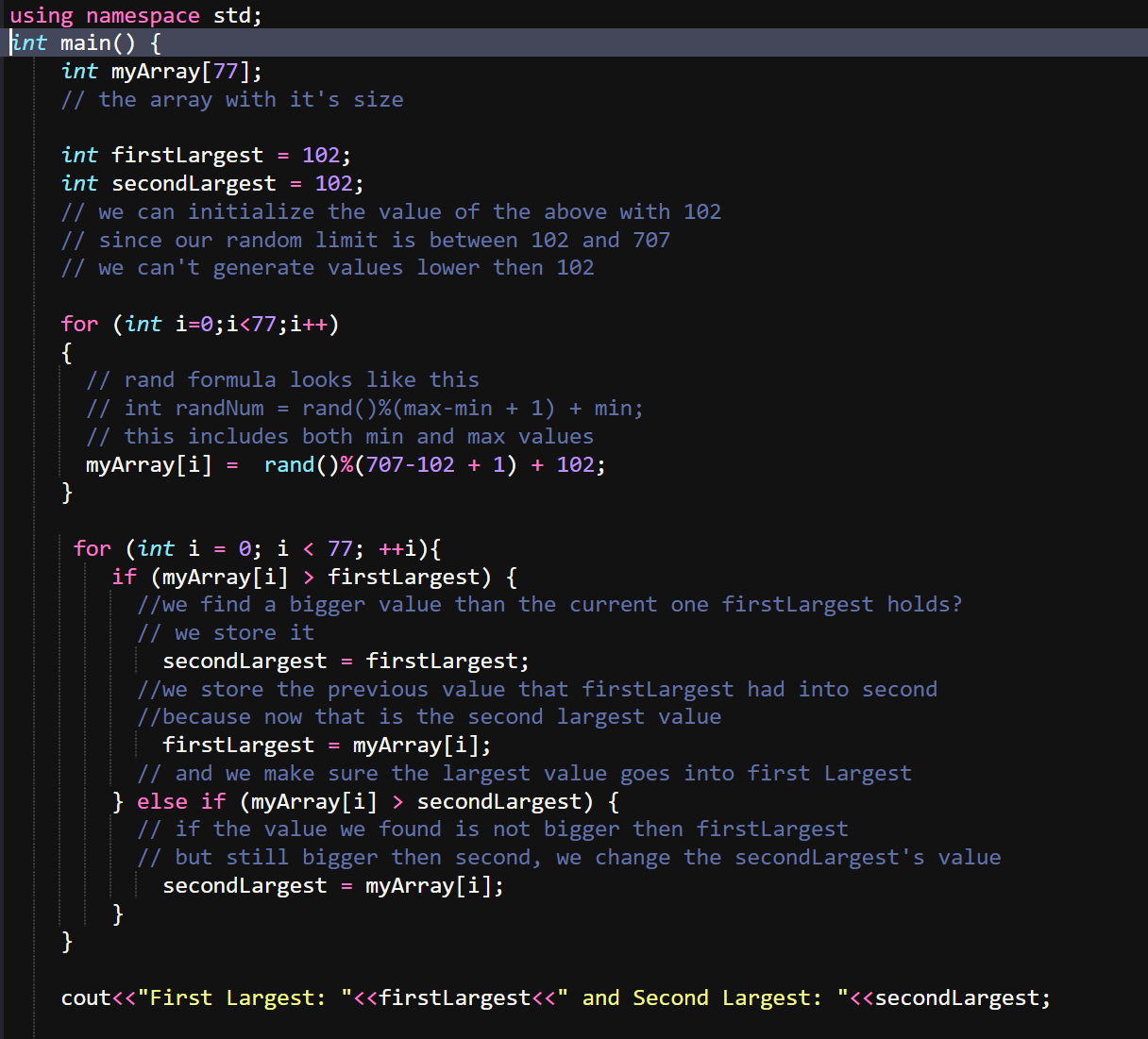
And the output:
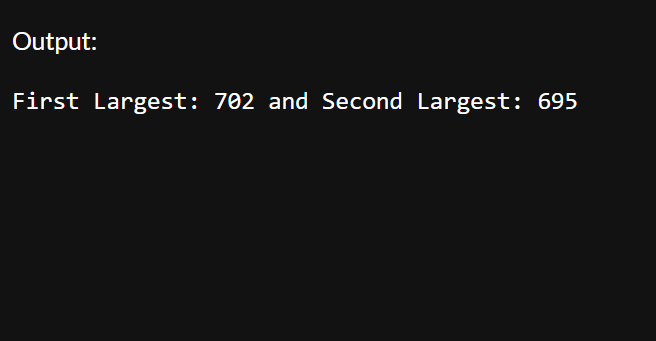
Sometimes you might need to take negative numbers into consideration, or zeros, but in this case the problem clearly states we have numbers between 102 and 707 so we don't need to add extra use cases. Also that's why we initialize our first and second largest with 102 because the problem states we can't get lower numbers.
Now depending on the problem the two largest numbers could be the same and in the end both numbers would still be the largest numbers in the array even though they are the same. But if the problem would state that these two could not be the same, we'd have to change the check and make sure these two numbers could not be the same.
Another approach to solve this problem could be by sorting the array and simply print the last two values.
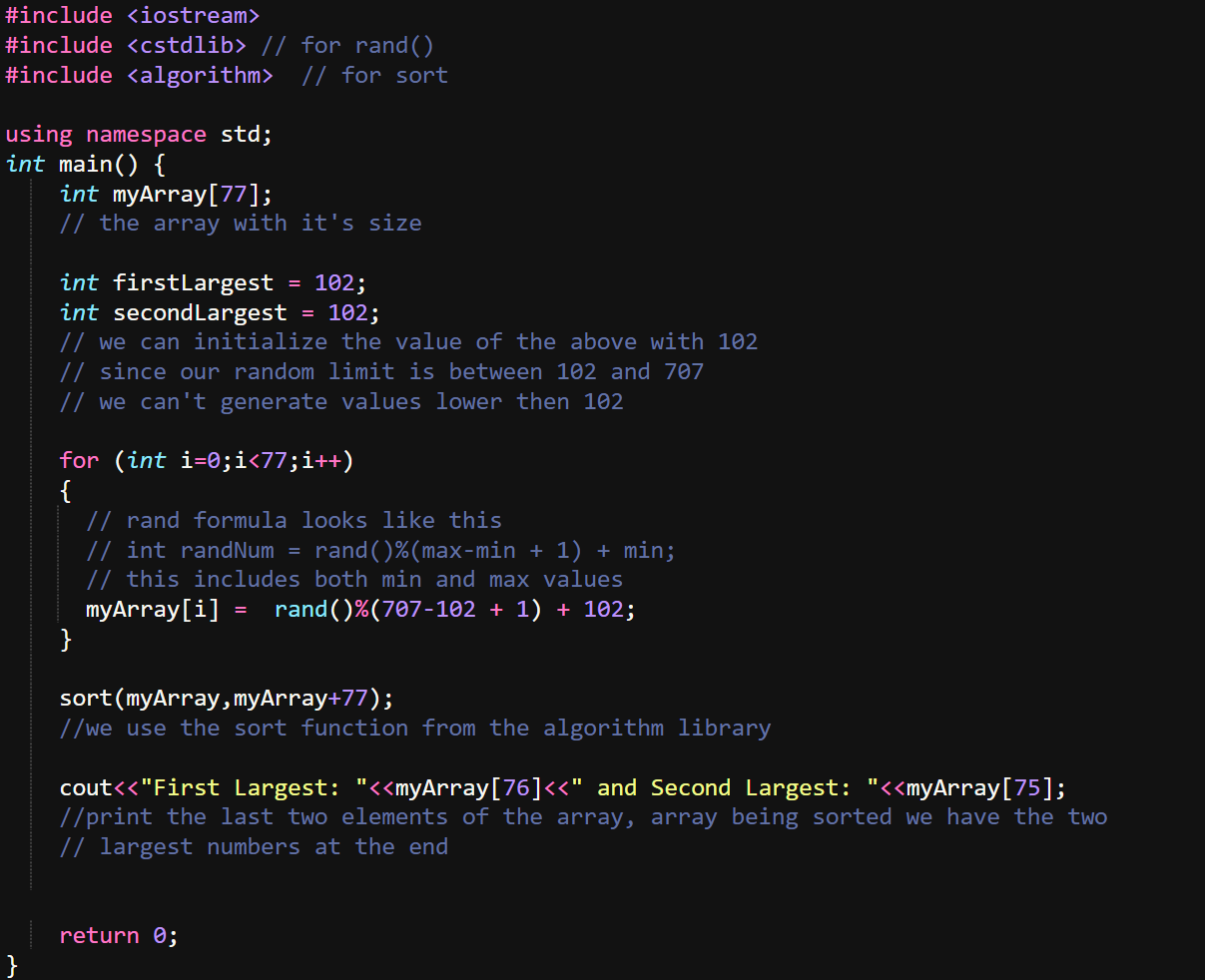
We could create our own sort function but why do that when you can call one from a library, we sorted the array and printed out the last two values, because it being sorted means we have the largest numbers at the end.
That was it for these tasks, hopefully I understood everything as intended, in the end I would like to invite @r0ssi, @titans and @mojociocio to join this.
Thank you @sergeyk for this class!
Comments